ACU-T: 3000 Enclosed Hot Cylinder: Natural Convection
This tutorial provides the instructions for setting up, solving and viewing results for a simulation of a hot cylinder contained within another air-filled cylinder. In this simulation, an internally heated cylinder is surrounded by air which heats up as it comes in contact with the surface of the inner cylinder. The localized heating near the surface induces a buoyancy driven flow in the air, generating convection currents. This tutorial is designed to introduce you to modeling concepts related to natural convection simulations.
- Creating and specifying a new custom material in AcuConsole
- Specifying a volume group as a heat source
- Using the Boussinesq density model in buoyancy driven flows, such as cases involving natural convection
- Set up periodic boundary conditions
- Analyze the problem
- Start AcuConsole and create a simulation database
- Set general problem parameters
- Set solution strategy parameters
- Create a new custom material model in AcuConsole and assign material properties to it
- Import the geometry for the simulation
- Create a volume group and apply volume parameters
- Create surface groups and apply surface parameters
- Set global and local meshing parameters
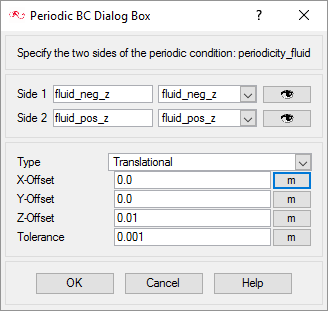
- Set periodic boundary conditions
- Generate the mesh
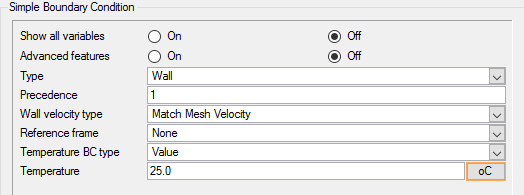
- Set the appropriate boundary conditions
- Run AcuSolve
- Monitor the solution with AcuProbe
- Post-processing the nodal output with AcuFieldView
Prerequisites
You should have already run through the introductory tutorial, ACU-T: 2000 Turbulent Flow in a Mixing Elbow. It is assumed that you have some familiarity with AcuConsole, AcuSolve, and AcuFieldView. You will also need access to a licensed version of AcuSolve.
Prior to running through this tutorial, copy AcuConsole_tutorial_inputs.zip from <Altair_installation_directory>\hwcfdsolvers\acusolve\win64\model_files\tutorials\AcuSolve to a local directory. Extract twin_cylinder.x_t from AcuConsole_tutorial_inputs.zip.
The color of objects shown in the modeling window in this tutorial and those displayed on your screen may differ. The default color scheme in AcuConsole is "random," in which colors are randomly assigned to groups as they are created. In addition, this tutorial was developed on Windows. If you are running this tutorial on a different operating system, you may notice a slight difference between the images displayed on your screen and the images shown in the tutorial.
Analyze the Problem
An important step in any CFD simulation is to examine the engineering problem at hand and determine the important parameters that need to be provided to AcuSolve. Parameters can be based on geometrical elements (such as inlets, outlets, or walls) and on flow conditions (such as fluid properties, velocity, or whether the flow should be modeled as turbulent or as laminar).
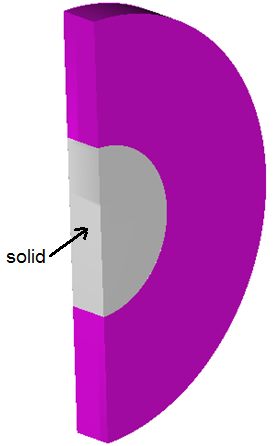
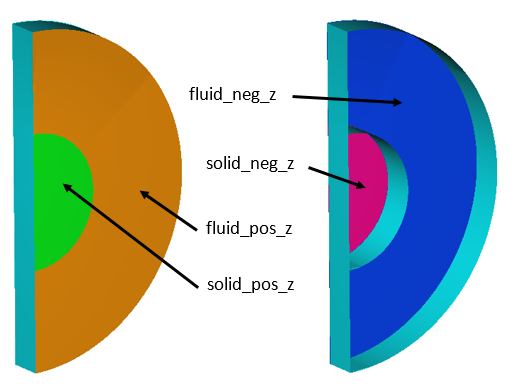
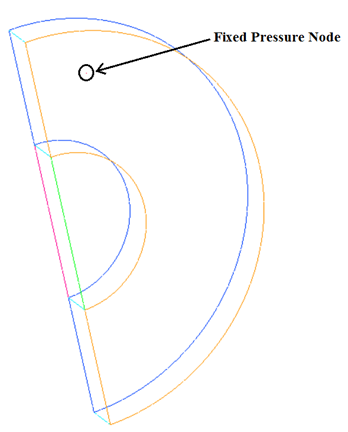
The system being simulated contains an internally-heated cylinder, which is surrounded by a cylindrical ring of a larger diameter. The annular volume between the two cylinders is filled with a fluid (air). The inner cylinder thus acts a heat source, and the fluid in contact with the surface of this heat source is heated up. This hot fluid, being lower in density than the cold fluid, then rises up to the upper part of the annulus due to buoyancy effects, and displaces the cold fluid at top. At the same time, the film of fluid which was in contact with the heating surface is replaced by the surrounding cold fluid. This new film of cold fluid goes through the same process until eventually a steady state convection current is achieved, or the inner cylinder ceases to generate heat and slowly the whole system achieves an equal temperature.
The system being simulated can be considered similar to a heat exchanger wherein the inner cylinder is akin to a tube through which a hot fluid passes by, and the air which surrounds this inner tube extracts heat from the inner tube. Another analogy can be of a wire carrying high current enclosed in an air cooled chamber. As the current heats up the wire due to resistance, the air around the wire keeps the wire temperature within control by extracting heat from the wire surface.

Figure 1. Schematic of the Problem
Introduction to Theory
Natural Convection
Convection is a heat transfer mechanism where the transfer of heat energy happens through the motion of matter. Since the definition of convection involves motion of matter a fluid state is usually present in convection. Usually this type of heat transfer takes place between a hot or a cold surface and a fluid. The film of fluid in contact with the surface absorbs heat from or transfers heat to the surface and is then replaced by a new film. This movement of fluid may either be governed by an external source, such as a fan or pump, or due to internal changes in the fluid properties. When no external sources are responsible for the fluid motion the heat transfer mechanism at work is called the Natural Convection. The driving force for motion of the fluid in a natural convection is density changes in the fluid due to temperature gradients induced in the fluid by heat transfer.
The natural convection mechanism works similarly as described above, whilst discussion of the problem. The fluid which is in contact with the surface absorbs or transfers heat from the surface and becomes hotter or colder than the surrounding fluid. Driven by buoyancy forces due to difference in densities caused by the temperature gradient, the fluid is displaced upwards or downwards. Surrounding fluid fills in the void created by the displaced fluid, which then undergoes the same process again. This gives rise to a convection current which drives the hot fluid to the top and cold fluid to the bottom of the convection cell. Buoyancy effects are driven by gravity, therefore natural convection requires presence of a gravitational force to work. It must be noted, however, that gravity is not the driving force behind the fluid movement. Presence of gravity only enables displacement of the fluid due to the density changes caused by temperature gradients.
Mathematical determination of the onset of natural convection is done through a dimensionless number called the Rayleigh number (Ra). The Rayleigh number is defined as:
- x is the characteristic length (m)
- is the Rayleigh number for characteristic length x
- is acceleration due to gravity (m/s2)
- is the surface temperature (K)
- is the quiescent temperature (fluid temperature far from the surface of the object) (K)
- is the kinematic viscosity (m2/s)
- α is the thermal diffusivity (m2/s)
- β is the thermal expansion coefficient (equals to for ideal gases where is absolute temperature).
The fluid properties , α and β are evaluated at the film temperature, , which is defined as:
When the Rayleigh number is below a critical value for the fluid heat transfer is primarily in the form of conduction. When it exceeds this critical value the dominant heat transfer mechanism is convection.
Boussinesq Density Model
The Boussinesq density model is an approximation method applied to buoyancy driven flows, such as natural convection flows. In the Boussinesq approximation, the density variation terms are neglected everywhere except when multiplied by acceleration due to gravity, . The basis of this approximation is that since temperature changes are small, the resultant changes in density are small as well and thus can be neglected. However, when multiplied by , the resultant term gives rise to forces which no longer are negligible. The Boussinesq approximation is:
- is the instantaneous density at temperature (kg/m3)
- is the density at reference temperature (kg/m3)
- is change in temperature (K)
As stated in the approximation, the Boussinesq density model is only applicable when density variations are small. A general guideline is to check for the condition to be true. This indirectly puts a limitation on this model to be used to only for cases where expected temperature differences within the fluid are not large.
Define the Simulation Parameters
Start AcuConsole and Create the Simulation Database
In this tutorial, you will begin by creating a database, populating the geometry-independent settings, loading the geometry, creating volume and surface groups, setting group parameters, adding geometry components to groups, and assigning mesh controls and boundary conditions to the groups. Next, you will generate a mesh and run AcuSolve to solve for the number of time steps specified. Finally, you will visualize some characteristics of the results using AcuFieldView.
In the next steps you will start AcuConsole, and create the database for storage of the simulation settings.
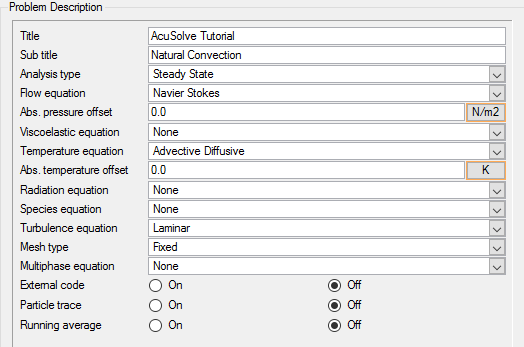
Set General Simulation Parameters
In next steps you will set parameters that apply globally to the simulation. To make this simple, the basic settings applicable for any simulation can be filtered using the BAS filter in the Data Tree Manager. This filter enables display of only a small subset of the available items in the data tree and makes navigation of the entries easier.
Set Solution Strategy Parameters
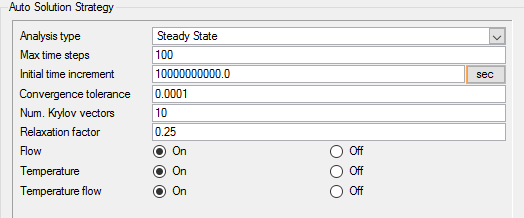
In the next steps you will set the parameters that control the behavior of AcuSolve as it progresses during the solution.
Set Material Model Parameters
Import the Geometry and Define the Model
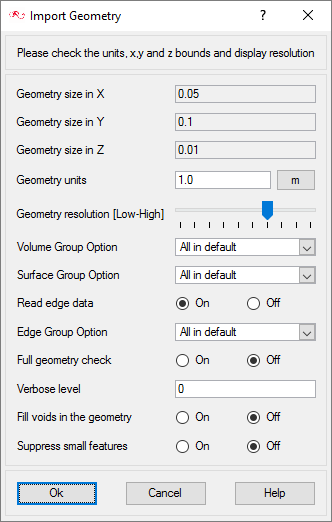
Import the Geometry
Set the Body Force
The body force commands add volumetric source terms to the governing conservation equations. Two types of body forces will be used in this tutorial.
The first one is the gravitational force on the fluid due to inertia of the fluid. As discussed in Analyze the Problem, gravity is an important aspect of the simulation. In fact, for thermal problems solved in AcuSolve with the Boussinesq approximation, the gravity is scaled by the product of the expansivity and the temperature minus reference temperature, while density remains constant. This variation in the gravitational force on fluid regions with different temperatures is what generated convection currents. For this tutorial gravity is defined as equal to standard gravity (g = 9.81 m/s2) along the negative Y-axis, which is the downward direction in the model.
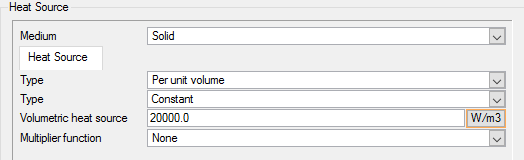
The second body force which will be used in this model is the volumetric heat source, which specifies the heat energy source term per unit volume. This will be used to simulate the heat-generating inner cylinder in our model.
Apply Volume Parameters
Volume groups are containers used for storing information about a volume region. This information includes solution and meshing parameters applied to the volume and the geometric regions that these settings are applied to.
When the geometry was imported into AcuConsole, all volumes were placed into the "default" volume container.
In the next steps you will create volume groups for each volume in the model, assign volumes to the respective volume groups, rename the default volume group container, and set the materials and other properties for each volume group.
Create Surface Groups and Apply Surface Parameters
Surface groups are containers used for storing information about a surface, including solution and meshing parameters, and the corresponding surface in the geometry that the parameters will apply to.
In the next steps you will define surface groups, assign the appropriate settings for the different characteristics of the problem, and add surfaces to the group containers.
In the process of setting up a simulation, you need to move into different panels for setting up the boundary conditions, mesh parameters, and so on, which can sometimes be cumbersome, especially for models with too many surfaces. To make it easier, less error prone, and to save time, two new dialogs are provided in AcuConsole. Use the Volume Manager and Surface Manager to verify and provide the information for all surface or volume entities at once. In this section some features of Surface Manager are exploited.
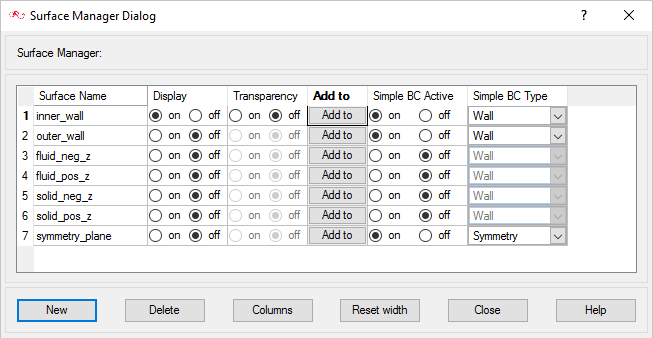
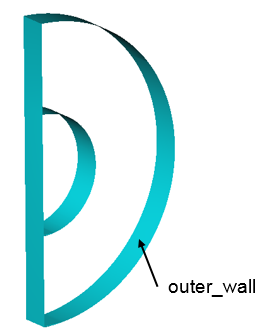
When the geometry was loaded into AcuConsole, all geometry surfaces were placed in the default surface group container. This default surface group was renamed to inner_walls. In the previous steps, you assigned some surfaces to various other surface groups that you created. At this point, all that is left in the inner_walls surface group are the surfaces which make up the contact boundary between the inner cylinder and the fluid volume.
Assign Surface Parameters
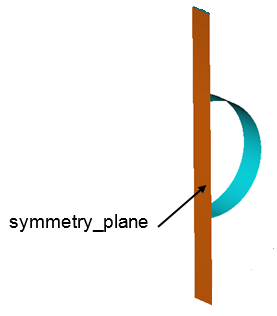
The modeling for this simulation was done using half symmetry. The model is only a partial representation of the system, the complete geometry of which is a cylinder. Hence it is appropriate to set the surface that you chose as symmetry_plane with a symmetry boundary condition to simulate that effect.
This change was completed using the Surface Manager in the last section. The following steps are thus optional.
Create Time History Output Points
Time History Output commands enables you to extract the nodal solution at any point within the domain.
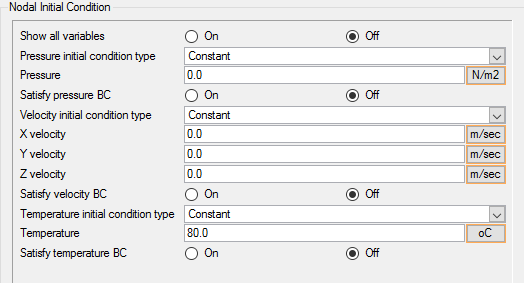
Set the Initial Conditions
Assign Mesh Controls
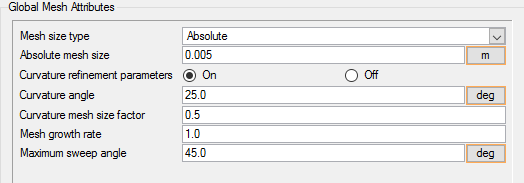
Set Global Mesh Parameters
Now that the flow characteristics have been set for the whole problem, a sufficiently refined mesh has to be generated.
Global mesh attributes are the meshing parameters applied to the model as a whole without reference to a specific geometric volume, surface, edge, or point. Local mesh attributes are used to create mesh generation controls for specific geometry components of the model.
In the next steps you will set the global mesh attributes.
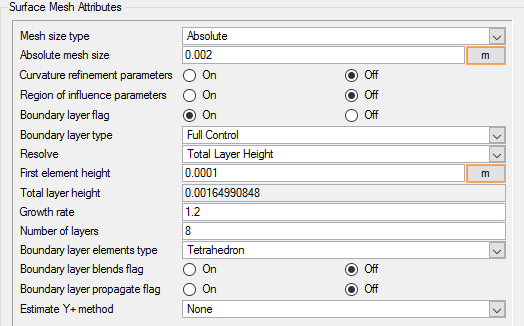
Set Surface Mesh Parameters
Surface mesh attributes are applied to a specific surface in the model. It is a type of local meshing parameter used to create targeted mesh controls for one or more specific surfaces.
Setting local mesh attributes, such as surface mesh attributes, is not mandatory. When a local mesh attribute is not found for a component, the global attributes are used as the mesh generation control for that component. If a local mesh attribute is present, it will take precedence over the global setting.
In the next steps you will set the surface meshing attributes.
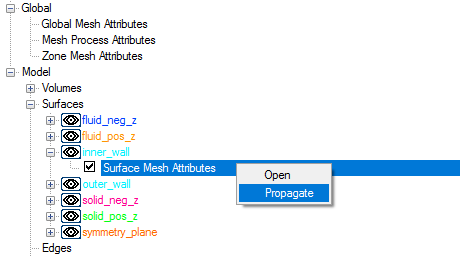
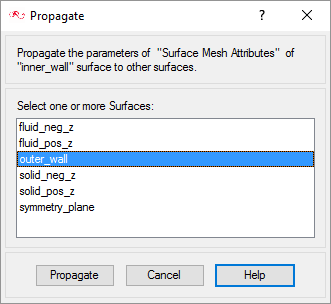
Instead of repeating the above steps for the outer_wall surface, you can choose to propagate the mesh attribute settings for inner_wall surface group to outer_wall surface group.
Define Mesh Extrusion
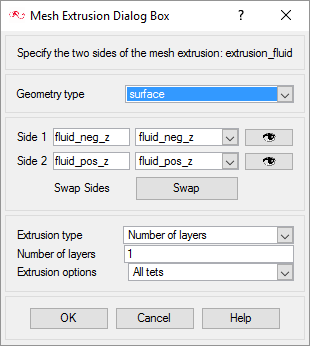
The present simulation is equivalent to a 2D representation of the model, which actually extends infinitely in both sides along the z-direction. In AcuSolve, 2D models are simulated by having just one element across the faces of the cross section. Thus when these faces are set up with a similar boundary condition, it coerces the corresponding nodes across the faces to have same results. In this problem, these faces are the negative and positive z-surfaces. This kind of mesh is achieved in AcuSolve with mesh extrusion process. In the following steps, the process of extrusion of the mesh between these surfaces is defined.
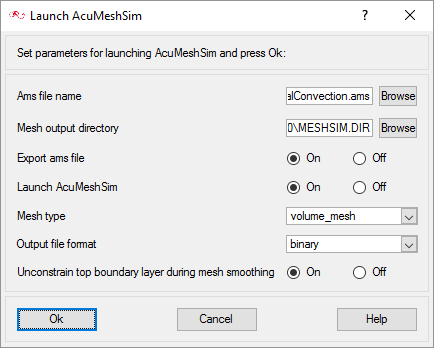
Generate the Mesh
In the next steps you will generate the mesh that will be used when computing a solution for the problem.
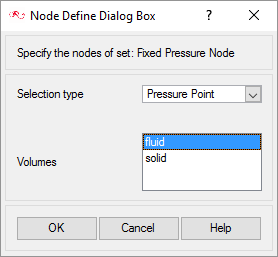
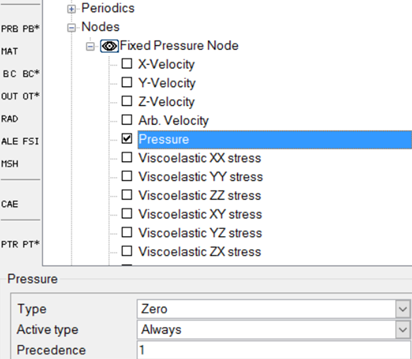
Assign Reference Pressure
The present case does not have any inlet or outlet surfaces to define any boundary condition that sets the pressure level inside the domain. To make the solution more robust, you will set a pressure reference point using a nodal boundary condition. The following steps will show how to setup the reference pressure inside the CFD domain.
Compute the Solution and Review the Results
Run AcuSolve
In the next steps you will launch AcuSolve to compute the solution for this case.
Post-Process with AcuProbe
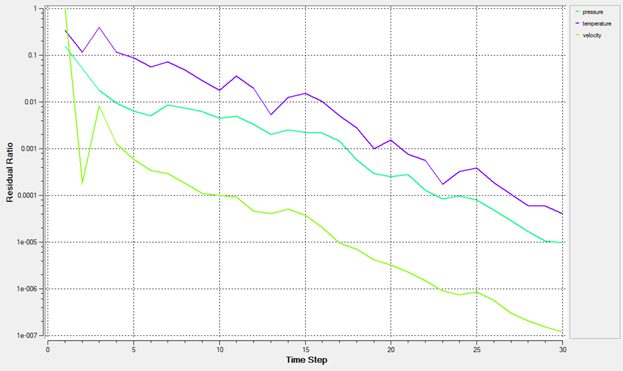
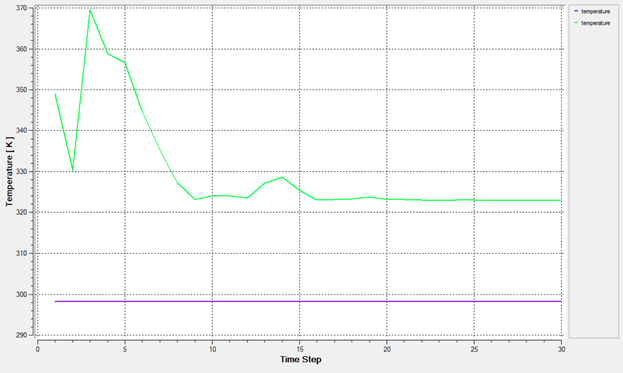
AcuProbe can be used to monitor various variables over solution time.
View Results with AcuFieldView
- How to find the data readers in the File menu and open up the desired reader panel for data input.
- How to find the visualization panels either from the toolbar or the Visualization panels from the main menu to create and modify surfaces in AcuFieldView.
- How to move the data around the modeling window using mouse actions to translate, rotate and zoom in to the data.
Start AcuFieldView
Manipulate the Model View in AcuFieldView
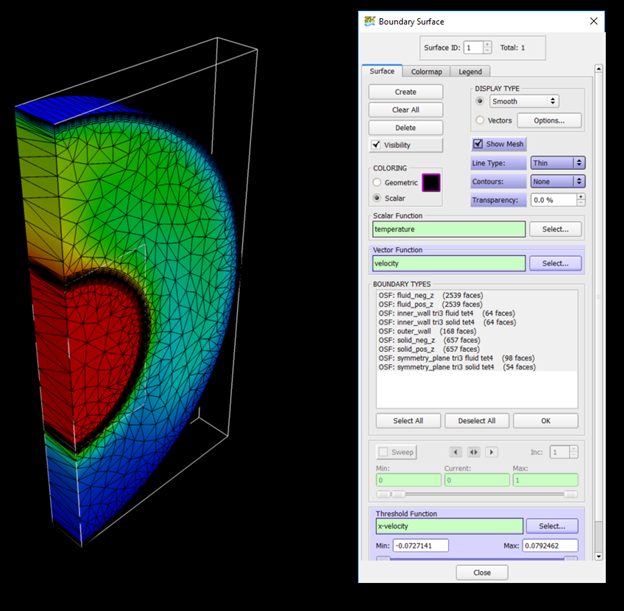
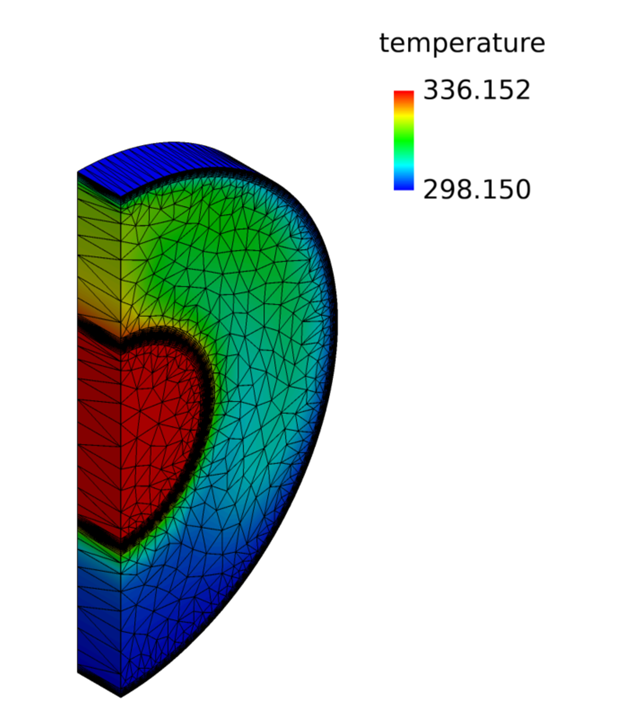
Create the Boundary Surface Showing Temperature for the Outer Surfaces with Mesh
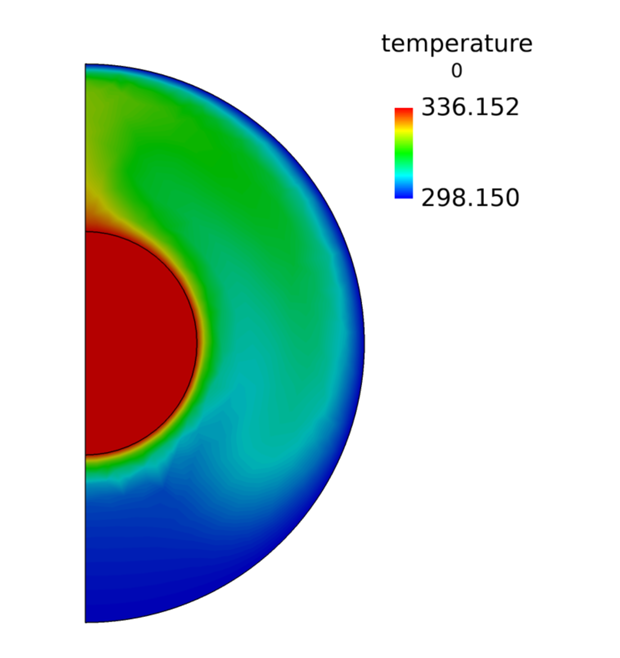
Coordinate the Surface Showing Temperature on the Mid-Coordinate Surface
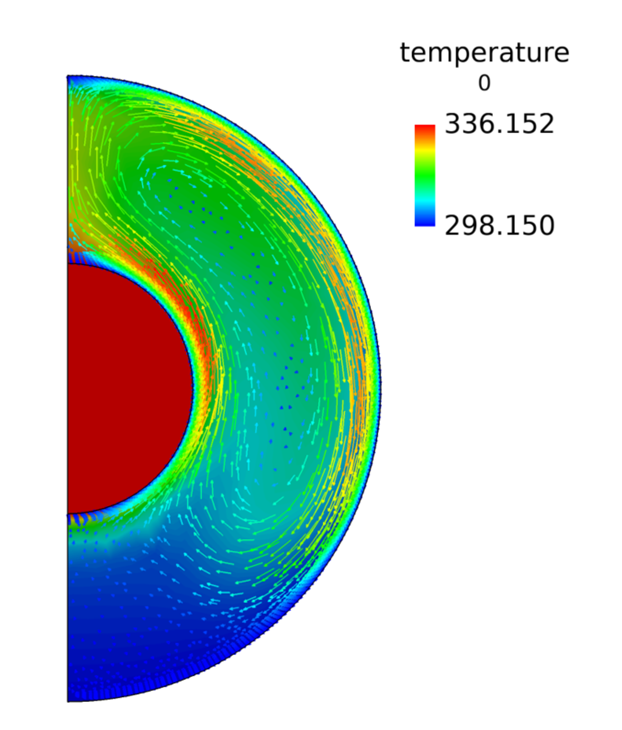
Coordinate the Surface Showing Vectors of Velocity on the Mid-Coordinate Surface
Summary
In this AcuSolve tutorial, you successfully set up and solved a natural convection problem. The problem simulated a hot cylinder placed in the center of another air-filled cylindrical volume. Air was modeled using a Boussinesq density approximation model, which is used for buoyancy driven flows, such as those involving natural convection. As the film of air in vicinity of the surface of the hot inner cylinder heated up, it generated convection currents within the annular volume.
You started the tutorial by creating a database in AcuConsole, importing and meshing the geometry and setting up the basic simulation parameters. The hot inner cylinder was represented by a solid volume also acting as a heat source. Once the case was setup, the solution was generated with AcuSolve.
Results were post-processed in AcuFieldView where you generated a temperature profile, and a velocity vector profile, on a cross-section of the model.
New features that were introduced in this tutorial include creating and specifying a new custom material in AcuConsole, specifying a volume group as a heat source using the Boussinesq density model and setting up periodic boundary conditions.