ACU-T: 3203 Heat Transfer Between Concentric Spheres – Discrete Ordinate Radiation Model
Prerequisites
This tutorial provides instructions for setting, solving and viewing results for a steady state simulation of radiation heat transfer between concentric spheres using the Discrete Ordinates Radiation model. Prior to starting this tutorial, you should have already run through the introductory HyperWorks tutorial, ACU-T: 1000 HyperWorks UI Introduction, and have a basic knowledge of HyperMesh, AcuSolve, and HyperView. To run this simulation, you will need access to a licensed version of HyperMesh and AcuSolve.
Prior to running through this tutorial, copy HyperMesh_tutorial_inputs.zip from <Altair_installation_directory>\hwcfdsolvers\acusolve\win64\model_files\tutorials\AcuSolve to a local directory. Extract ACU-T3203_DiscreteOrdinate.hm from HyperMesh_tutorial_inputs.zip.
Since the HyperMesh database (.hm file) contains meshed geometry, this tutorial does not include steps related to geometry import and mesh generation.
Problem Description
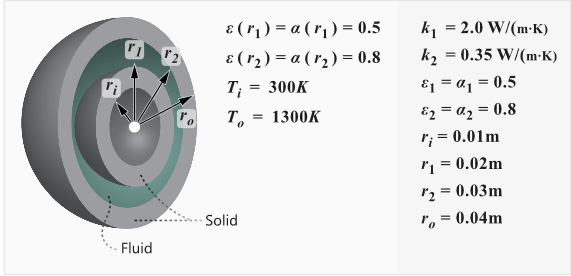
The problem to be addressed in this tutorial is shown schematically in Figure 1. In this problem, a DO radiation model is used to simulate the heat transfer due to radiation between concentric spheres. The inside surface of the inner and the outside surface of the outer sphere are both held at constant temperature while the gap between them radiates the heat from one sphere to the other.
The problem consists of a fluid region with arbitrary material properties between two concentric spheres with surfaces held at fixed temperature, as shown in the following figure, which is not drawn to scale. The radius of the outer sphere is 0.04 m and the radius of the inner sphere is 0.01 m. The inner surface of the inner sphere is defined to have a constant wall temperature at 300.0 K (26.85 ºC). The outer surface of the outer sphere is defined to have a constant wall temperature at 1300.0 K (1026.85 ºC). The fluid within the spheres is defined as a non-conducting material, allowing heat to transfer via radiation only.
The problem is solved as a steady state case to allow the heat transfer in the solid and fluid regions to reach an equilibrium.
Open the HyperMesh Model Database
Set the General Simulation Parameters
Set Up Radiation Parameters and Boundary Conditions
In this step, you will define the radiation parameters i.e. emissivity models, surface boundary conditions for the problem, and assign material properties to the fluid and solid regions.
Set Up Material Model Parameters
Set Up Emissivity Model Parameters
Set Up Boundary Conditions
Compute the Solution
In this step, you will launch AcuSolve directly from HyperMesh and compute the solution.
Run AcuSolve
Post-Process the Results with HyperView
Open HyperView and Load the Model and Results
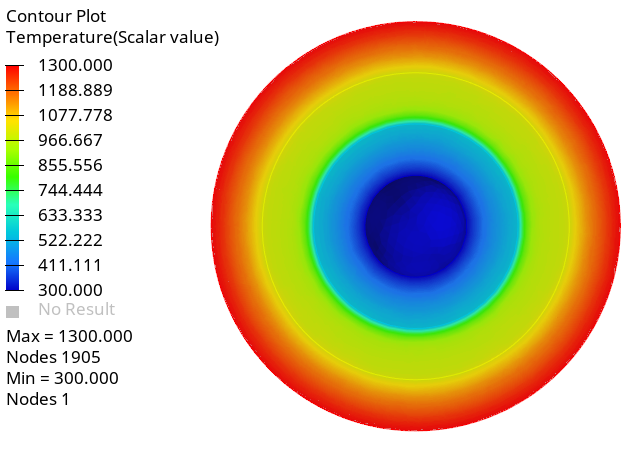
Create Temperature Contours
In this step, you will create a contour plot of temperature distribution across the domain.
Summary
In this tutorial, you worked through a workflow to set-up a DO-Radiation model, carry out a radiation heat transfer simulation, and post-process the results using HyperWorks products, namely AcuSolve, HyperMesh, and HyperView. You started by importing the model in Altair HyperMesh. Then you defined the simulation parameters and launched AcuSolve directly from within HyperMesh. Upon completion of the solution by AcuSolve, you used HyperView to post-process the results and create contour plots.