OS-E: 0896 Multi-Material Topology Optimization of Automotive Cradle

Multi-Material Optimization (MMO) can be used in applications that require optimizing the parts of different materials. This method offers an initial concept-level look at material placement within the structure, where multiple materials can be evaluated.

The relationship between the mass savings, stiffness, and relative cost to manufacture the material can be included in the optimization formulation.

Without a consistent formulation, optimization would favor the lightest or stiffest material (steel or aluminum) but competing requirements can guide the design.

Multi-material optimization can be used when information outside of the structural performance is known that would influence total production costs, such as the relative price of different materials, and the relative volume production of each of them.

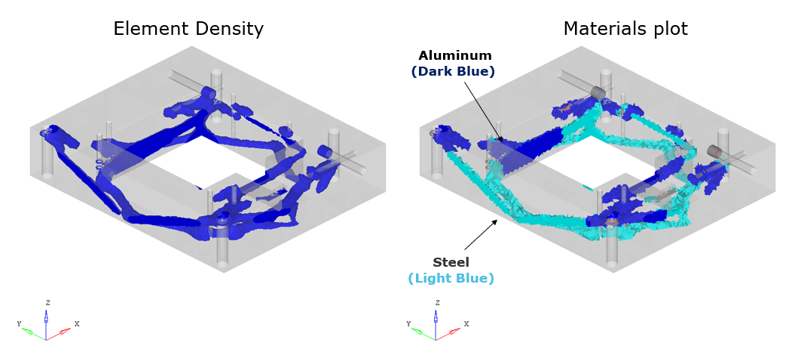
Consideration to include manufacturing constraints can help guide the resulting structures to be better produced by traditional methods.
  • Case 1:

    Objective: Topology optimization to minimize the mass considering multiple materials (steel + aluminum)

    The optimization result includes both materials, steel, and aluminum, placed at the optimal locations.

  • Case 2:

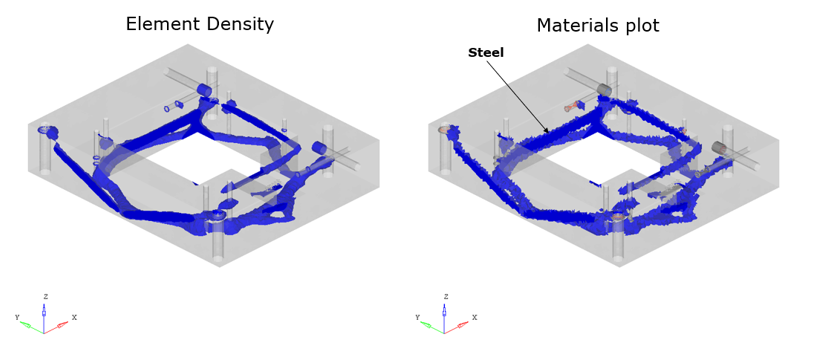
    Objective: Topology optimization to minimize the relative maximum between mass and cost considering multiple materials.

    It is considered that aluminum is 1.5 times more expensive per mass than steel using the function f ( x , y ) = x + 1.5 ∗ y MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm aabaGaamiEaiaacYcacaWG5baacaGLOaGaayzkaaGaeyypa0JaamiE aiabgUcaRiaaigdacaGGUaGaaGynaiabgEHiQiaadMhaaaa@4213@ .

    The optimization result favors the cheaper material, in this case, steel, no aluminum is used, due to cost.

  • Case 3:

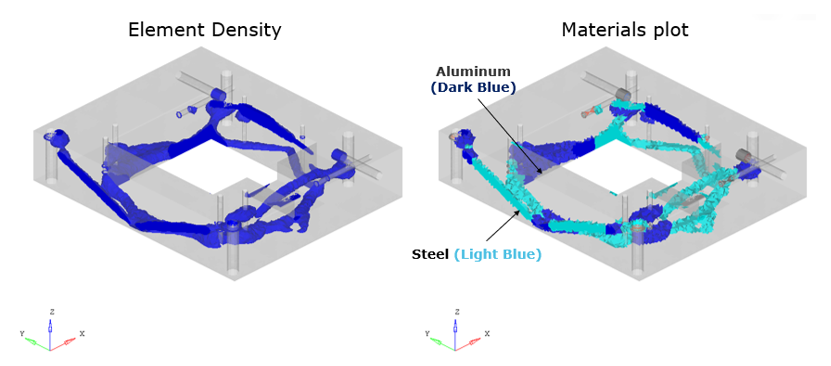
    Objective: Topology optimization to minimize the relative maximum between mass and cost considering multiple materials, as well as retaining a certain amount of steel.

    It is considered that aluminum is 1.5 times more expensive than steel using the function f ( x , y ) = x + 1.5 ∗ y MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm aabaGaamiEaiaacYcacaWG5baacaGLOaGaayzkaaGaeyypa0JaamiE aiabgUcaRiaaigdacaGGUaGaaGynaiabgEHiQiaadMhaaaa@4213@ .

    Optimization gives both steel and aluminum, since the mass of steel is limited to 80% of the total mass.

Model Description

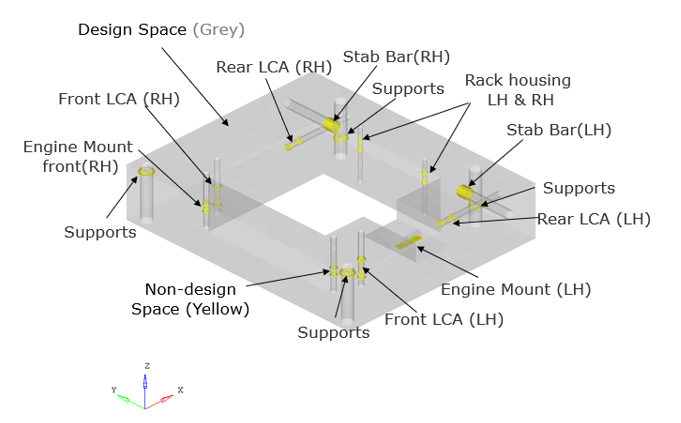
In this example, Multi-Material Topology Optimization is performed on the automotive cradle (aluminum + steel) model with 3 different objectives to fulfill.


Figure 1. Cradle Model with Constraints and Loading Conditions
  • Unit loads are applied at 10 locations in X, Y, and Z directions
  • Displacement constraints are applied at all the loading conditions, measured from the existing design
FE Model
Cradle body
CTETRA
Connectors
Rigid elements (RBE2)
Linear Material Properties (MAT1)
Aluminum
Young's modulus
7E+04 MPa
Poisson's ratio
0.29
Density
2.7E-09 ton/mm3
Steel
Young's modulus
1.95E+05 MPa
Poisson's ratio
0.29
Density
9E-09 ton/mm3

Results



Figure 2. Case 1 Topology Optimization Results


Figure 3. Case 2 Topology Optimization Results


Figure 4. Case 3 Topology Optimization Results

Model Files

The model files used in this example include:

<install_directory>/hwsolvers/demos/optistruct/examples
  • /case1.fem
  • /case2.fem
  • /case3.fem