Particle Kinematics
Kinematics deals with position in space as a function of time and is often referred to as the "geometry of motion". 1 The motion of particles may be described through the specification of both linear and angular coordinates and their time derivatives. Particle motion on straight lines is termed rectilinear motion, whereas motion on curved paths is called curvilinear motion. Although the rectilinear motion of particles and rigid bodies is well-known and used by engineers, the space curvilinear motion needs some feed-back, which is described in the following section.
Space Curvelinear Motion
Where,
vr=˙r
vθ=r˙θ
vz=˙z
Where,
ar=¨r−r˙θ2
aθ=r¨θ+2˙r˙θ
az=¨z
Where,
vR=˙R
vθ=R˙θ cosφ
vφ=R˙φ
Where,
aR=¨R−R˙φ2−R˙θ2cos2φ
aθ=cosφRddt(R2˙θ)−2R˙θ˙φ sinφ
aφ=1Rddt(R2˙φ)+R˙θ2 sinφ cosφ
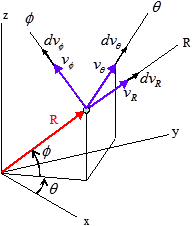
Coordinate Transformation
or {Vrθz}=[Tθ]{Vxyz}
or {VRθϕ}=[Tϕ]{Vrθz}
with: [Tϕ][Tθ]=[cosϕcosθ cosϕsinθsinϕ−sinθcosθ0−sinϕcosθ−sinϕsinθcosϕ]
Reference Axes Transformation
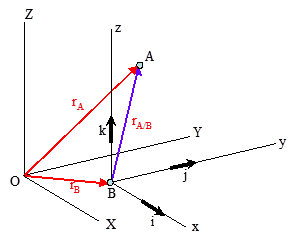
=(Vxddt( ˆi)+Vyddt( ˆj) +Vzddt( ˆk))+(˙Vxˆi+˙Vyˆj +˙Vzˆk)
This equation establishes the relation between the time derivative of a vector quantity in a fixed system and the time derivative of the vector as observed in the rotating system.

Where, the term 2ω×vrel constitutes Coriolis acceleration.
Skew and Frame Notations
- Skew Reference
- A projection reference to define the local quantities with respect to the global reference. In fact the origin of skew remains at the initial position during the motion even though a moving skew is defined. In this case, a simple projection matrix is used to compute the kinematic quantities in the reference.
- Frame Reference
- A mobile or fixed reference. The quantities are computed with respect to the origin of the frame which may be in motion or not depending to the kind of reference frame. For a moving reference frame, the position and the orientation of the reference vary in time during the motion. The origin of the frame defined by a node position is tied to the node. Equation 22 and Equation 26 are used to compute the accelerations and velocities in the frame.