Mount Limits
The Altair Bushing Model includes a Mount Limits feature, which lets you model the material contact that occurs between the bodies that a bushing connects. The bodies are flexible and may deflect under the load being transmitted. Given enough bushing deflection, the bodies may contact one another for negative and positive deflections in each direction.
When bushings deflect, a large amount of contact can occur between the bodies they connect limiting the deflection. However, these limits are dependent on the geometry of the bodies and are not an intrinsic bushing property. Therefore mount limits are specified in a separate Mount Limits Property File (*.gbi). In this file you can:
- Activate mount limits for a bushing.
- Define gap, stiffness and damping properties that are appropriate for the bodies that the bushing connects.
When the bushing deflection closes the gap between the bodies in a specific direction, the mount limit in the corresponding direction exerts a force or torque to limit the deflection. The following image shows how such a contact can occur at the connection between the A-Arm and the Strut in a suspension.
The mount limit force or torque adds to the bushing force or torque and acts to increase the normal force or torque input to the bushing friction and the local deflection of the bodies.
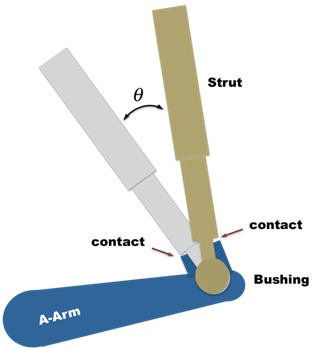
Mount Limits depend on the geometry of the bodies that mount the bushing, and not the bushing itself. Therefore, the displacement and velocity used for computing the mount limit forces and moments, unlike the bushing, is not scaled, offset or coupled.
You can define positive and negative mount limits for any set of bushing directions: {FX, FY, FZ, TX, TY, and TZ}.
- A positive mount limit acts to limit positive displacement in a given direction by producing a negative force or torque.
- A negative mount limit acts to limit bushing negative displacement and produces a positive force or torque.
- All the input parameters like stiffness, gap, and exponent for either positive or negative mount limits are always entered as positive values.
Positive Mount Limits
Let:
- qk and ˙qk
- be displacement and velocity between the I body and J body less any local structural deflection as computed by the mount-stiffness CONTROL_STATEEQN.
- Lk
- be the gap that must be closed for material contact to occur.
- Kk
- be the stiffness of the limit.
- Ek
- be the exponent applied to the deflection. Ek ≥ 1.0 to ensure a constant or rising stiffness rate with deflection.
- Ck
- be the damping coefficient.
- Dk
- be the deflection at which the damping is fully active. For deflections less then Dk , the damping force is modified by the step function to prevent discontinuity of the contact force.
Then the force or torque in the kth direction for a positive mount limit is defined as:
if (Mount_Limits_Are_Inactive OR qk≤Lk)
Fk = 0.0
else
Fk=min(0.0, −Kk(qk−Lk)Ek −Ck˙qk Step(qk−Lk, 0.0, 0.0, Dk, 1.0))
Negative Mount Limits
For a negative mount limit, the limit force is computed in the same manner as a positive mount limit, however the input displacement and velocity are negated as is the output force. Again all the input parameters are positive. The force/torque computation for a negative mount limit is:
if (Mount_Limits_Are_Inactive OR qk≥Lk)
Fk = 0.0
else
Fk=−min(0.0, −Kk(−qk−Lk)Ek −Ck(−˙qk) Step(-qk−Lk, 0.0, 0.0, Dk, 1.0))