MV-7002: Co-simulation with Simulink

In this tutorial, you will learn how to use the MotionSolve-Simulink co-simulation interface, driving the model from Simulink via an S-Function. MotionSolve co-simulates with Simulink using the Inter Process Communication (IPC) approach.

In IPC co-simulation, the two solvers are run on two separate processes with data being exchanged through sockets.

Software and Hardware Requirements

Software requirements:

MotionSolve
MATLAB/Simulink (MATLAB Version R2015a), Simulink Version 8.5) (or newer)

Note: Older versions of MATLAB/Simulink may work, but the above minimum versions are recommended and tested

Hardware requirements:

PC with 64-bit CPU, running Windows 7/10 or higher
Linux RHEL 6.6 or CentOS 7.2
Note: MATLAB R2019a and higher require Windows 10 and RHEL 7.8.

Inverted Pendulum Controller

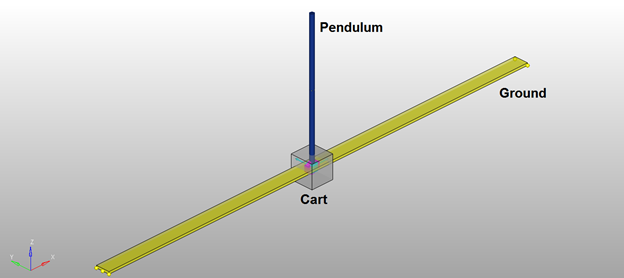
Consider an inverted pendulum, mounted on a cart. The pendulum is constrained at its base to the cart by a revolute joint. The cart is free to translate along the X direction only. The pendulum is given an initial rotational velocity causing it to rotate about the base.

Both the pendulum and the cart are modeled as rigid bodies. The controller, modeled in Simulink, provides a control force to the cart to stabilize the inverted pendulum and prevent it from falling. This control force is applied to the cart via a translational force. The model setup is illustrated in the figure below.

Figure 1. Inverted Pendulum Model Setup

The pre-designed controller generates a control force that keeps the pendulum upright. The controller uses the pendulum's orientation and angular velocity along with the cart's displacement and velocity as inputs to calculate the direction and magnitude of the force needed to keep the pendulum upright. A block diagram of the control system is shown below.

In the image above:

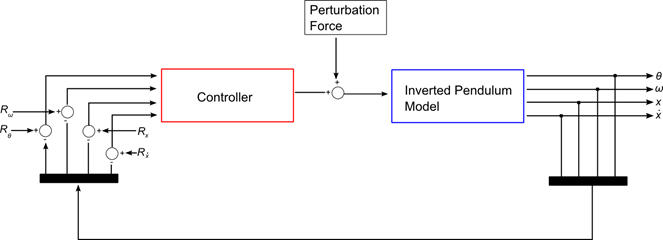
$θ$ is the angular displacement of the pendulum from its model configuration
$ω$ is the angular velocity of the pendulum about its center of gravity as measured in the ground frame of reference
$x$ is the translational displacement of the cart measured from its model configuration in the ground frame of reference
$\dot{x}$ is the translational velocity of the cart measured in the ground frame of reference
$R_{θ}$ is a reference signal for the pendulum's angular displacement
$R_{ω}$ is a reference signal for the pendulum's angular velocity
$R_{x}$ is a reference signal for the cart's translational displacement
$R_{\dot{x}}$ is a reference signal for the cart's translational velocity

A disturbance is added to the computed control force to assess the system response. The controller force acts on the cart body to control the displacement and velocity profiles of the cart mass.

In this exercise, you will do the following:

Solve the baseline model in MotionSolve only (that is, without co-simulation) by using the inverted pendulum model with a continuous controller modeled by a Force_Vector_OneBody element. You can use these results to compare to an equivalent co-simulation in the next steps.
Review a modified MotionSolve inverted pendulum model that mainly adds the Control_PlantInput and Control_PlantOutput entities that allow this model to act as a plant for Simulink co-simulation.
Review the controller in Simulink.
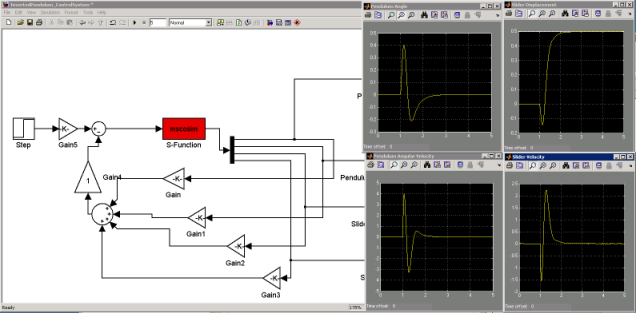
Perform a co-simulation and compare the results between the standalone MotionSolve model and the co-simulation model.

Before you begin, copy all the files in the <installation_directory>\tutorials\mv_hv_hg\mbd_modeling\motionsolve\cosimulation folder to your working directory (referenced as <working directory> in the tutorial). Here, <altair> is the full path to the HyperWorks installation.

Run the Baseline MotionSolve Model

In this step, use a single body vector force (Force_Vector_OneBody) to model the control force in MotionSolve. The force on the cart is calculated as:

$F_{c a r t} = F_{c o n t r o l} + F_{d i s t}$ , where

$F_{d i s t}$ is the disturbance force,

$F_{c o n t r o l} = K_{1} (e r r o r_{θ}) + K {}_{2}{(e r r o r_{ω})} + K_{3} (e r r o r_{x}) + K_{4} (e r r o r_{\dot{x}})$ is the control force,

$K_{i}$ are gains applied to each of the error signals

$e r r o r$ is the error (difference between reference and actual values) on the input signals.

The angular displacement and velocity of the pendulum are obtained by using the AY() and WY() expressions respectively. The translational displacement and velocity of the cart are obtained similarly, by using the DX() and VX() expressions.

From the Start menu, select All Programs > HyperWorks <version> MotionView. Open the model InvertedPendulum_NoCosimulation.mdl from your <working directory>.

The MotionSolve model consists of the following components:

Component Name	Component Type	Description
Slider cart	Rigid body	Cart body
Pendulum	Rigid body	Pendulum body
Slider Trans Joint	Translational joint	Translational joint between the cart body and the ground
Pendulum Rev Joint	Revolute joint	Revolute joint between the pendulum body and the cart body
Control Force	Vector force	The control force applied to the cart body
Output control force	Output request	Use this request to plot the control force
Output slider displacement	Output request	Use this request to plot the cart's displacement
Output slider velocity	Output request	Use this request to plot the cart's velocity
Output pendulum displacement	Output request	Use this request to plot the pendulum's displacement
Output pendulum velocity	Output request	Use this request to plot the pendulum's velocity
Pendulum Rotation Angle	Solver variable	This variable stores the rotational displacement of the pendulum via the expression AY()
Pendulum Angular Velocity	Solver variable	This variable stores the rotational velocity of the pendulum via the expressionVY()
Slider Displacement	Solver variable	This variable stores the translational displacement of the cart via the expression DX()
Slider Velocity	Solver variable	This variable stores the translational velocity of the cart via the expression VX()

In the Run panel, specify the name InvertedPendulum_NoCosimulation.xml for the MotionSolve model name and click Run.
The results achieved will be used as the baseline to compare the results obtained from co-simulation.

Define the Plant in the Control Scheme

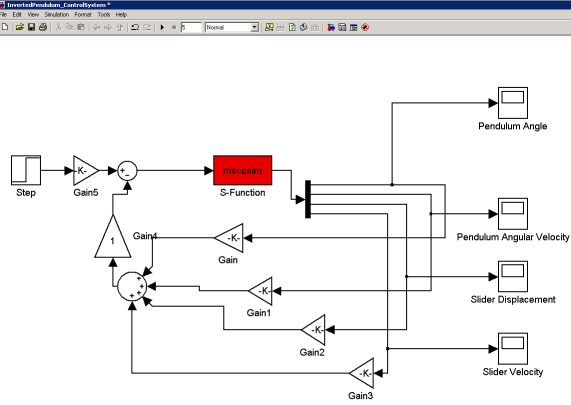
A MotionSolve model needs a mechanism to specify the input and output connections to the Simulink model. The MotionSolve model (XML) used above is modified to include the Control_PlantInput and Control_PlantOutput model elements and provide these connections. In this tutorial, this has already been done for you, and you can see this by opening the model InvertedPendulum_Cosimulation.mdl from your <working directory>.

This model contains two additional modeling components:

Component Name	Component Type	Description
Plant Input Simulink	Plant input	This Control_PlantInput element is used to define the inputs to the MotionSolve model
Plant Output Simulink	Plant output	This Control_PlantOutput element is used to define the outputs from the MotionSolve model

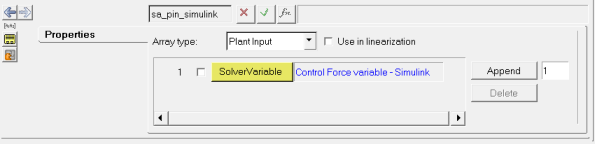
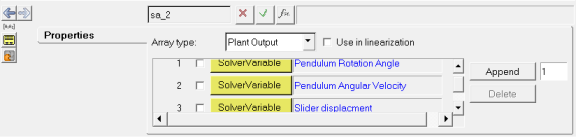
The Control_PlantInput element defines the inputs to a mechanical system or plant. For this model, only one input is defined in the "Plant Input Simulink" solver array. This is set to the ID of the solver variable that holds the control force from Simulink.

The Control_PlantOutput element defines the outputs from a mechanical system or plant. For this model, four outputs are defined in the "Plant Output Simulink" solver array. These are the pendulum rotation angle, the pendulum angular velocity, slider displacement and slider velocity.

The inputs specified using the Control_PlantInput and Control_PlantOutput elements can be accessed using the PINVAL() and POUVAL() functions, respectively. Since the Control_PlantInput and Control_PlantOutput list the IDs of solver variables, these input and output variables may also be accessed using the VARVAL() function. For more details, please refer to the MotionSolve User's Guide.

This model has the following connections:

Plant Input: A single control force that will be applied to the cart.
Plant Output: The pendulum's angular displacement and angular velocity; the cart's translational displacement and velocity.

Set Up Environment Variables

A few environment variables are needed for successfully running a co-simulation using MATLAB. These can be set using one of the following methods:

Control panel (Windows)
In the shell/command window that calls MATLAB (with the set command on Windows, or the export command on Linux)

Within MATLAB, via the setenv() command

An example of the usage of these commands is listed below:

Environment variable	Value	Windows shell	Linux shell	MATLAB shell
PATH	\mypath	set PATH=\mypath	setenv PATH \mypath	setenv('PATH','\mypath')

Set the following environment variables:

Environment variable	Path - Windows	Path - Linux
NUSOL_DLL_DIR	<altair>\hwsolvers\motionsolve\bin\win64	<altair>\hwsolvers\motionsolve\bin\linux64
RADFLEX_PATH	<altair>\hwsolvers\common\bin\win64	<altair>\hwsolvers\common\bin\linux64
PATH	<altair>\hwsolvers\common\bin\win64;%PATH%	<altair>\hwsolvers\common\bin\linux64:$PATH
LD_LIBRARY_PATH	-	<altair>\hwsolvers\motionsolve\bin\linux64 <altair>\hwsolvers\common\bin\linux64:$LD_LIBRARY_PATH

where <altair> is the full path to the HyperWorks installation. For example, on Windows, this would typically be C:\Program Files\Altair\<version>.

Note that other optional environment variables may be set for your model. See MotionSolve Environment Variables for more information on these environment variables.

Set Up the Co-simulation

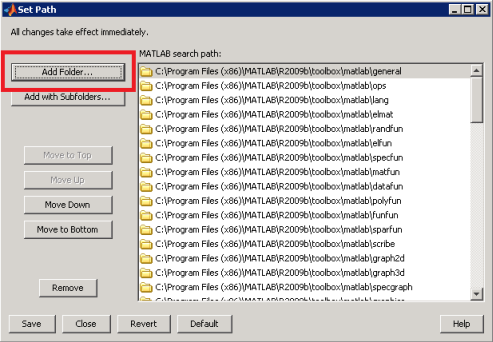
The core feature in Simulink that creates the co-simulation is an S-Function (System Function) block in Simulink. This block requires an S-Function library (a dynamically loaded library) to define its behavior. MotionSolve provides this library, but the S-Function needs to be able to find it. To help MATLAB/Simulink find the S-Function, you need to add the location of the S-Function to the list of paths that MATLAB/Simulink uses in order to search for libraries.

The S-Function library for co-simulation with MotionSolve is called mscosimipc – for Inter Process Communication (IPC) using TCP/IP sockets for communication. This file is installed under <altair>\hwsolvers\motionsolve\bin\<platform>.

The location of this file needs to be added to the search path of MATLAB for the S-Function to use mscosimipc.

This can be done in one of the following ways:

Use the menu options.
1. From the MATLAB menu, select File > Set Path.
  
  Figure 6. Add path through the MATLAB GUI
2. From the dialog, add the directory where the mscosimipc library resides.
  <altair>\hwsolvers\motionsolve\bin\win64
3. Select Save and Close.
  This procedure permanently adds this directory to the MATLAB/Simulink search path.
Use MATLAB commands.
1. To add the directory where mscosimipc library resides into the MATLAB search path, at the MATLAB command line, type
```
addpath('<altair>\hwsolvers\motionsolve\bin\<platform>')
```
  It remains valid until you exit MATLAB.
  Note: You can also create a .m script to make this process more easily repeatable.
  For example, you can set the MATLAB Path and the necessary environment variables using MATLAB commands in a MATLAB (.m) script:
  addpath('<altair>\hwsolvers\motionsolve\bin\win64') setenv('NUSOL_DLL_DIR','<altair>\hwsolvers\motionsolve\bin\win64') setenv('RADFLEX_PATH',['<altair>\hwsolvers\common\bin\win64') setenv('PATH',['<altair >\hwsolvers\common\bin\win64;' getenv('PATH')])
2. For a Linux machine, additionally enter
```
setenv('LD_LIBRARY_PATH', '<altair>\hwsolvers\motionsolve\bin\linux64:<altair>\hwsolvers\common\bin\linux64\') 
```

View the Controller Modeled in Simulink

In the MATLAB window, select File > Open.
The Open file dialog is displayed.
Select the InvertedPendulum_ControlSystem.mdl file from your <working directory>.
Click Open.
You will see the control system that will be used in the co-simulation.

Figure 7. The Control System in MATLAB
The model contains an S-function block. Name the S-function 'mscosim'. Double click on the S-Function named mscosim. In the dialog box that is displayed, change the name of the S-function to ‘mscosimipc’.

The S-function (system-function) is one of the blocks provided by Simulink and represents the MotionSolve model. It can be found in the Simulink User-Defined Functions block library. An S-Function allows you to model any general system of equations with inputs, outputs, states, and so on, and is somewhat analogous to a Control_StateEqn in MotionSolve. See the MATLAB/Simulink documentation for more details.
Double-click the S-function with name mscosimipc. In the dialog that is displayed, under the S Function Parameters, enter the following using single quotes:
```
' InvertedPendulum_Cosimulation.xml', 'InvertedPendulum_Cosimulation.mrf', ''
```
The three parameters are the following:
- MotionSolve XML model name
- Output MRF name
- MotionSolve user DLL name (optional); enter empty single quotes ('') if not used.

Repeat the Co-simulation

Click Simulation > Start to start the co-simulation.
Simulink uses ODE45 to solve the Simulink model. From this, the co-simulation should begin and MotionSolve should create an output .mrf file for post-processing.
Set the Scopes in the Simulink model to display the results.
Check the .log file to make sure no errors or warnings were issued by MotionSolve.

Figure 8.

Compare the MotionSolve-only Results to the Co-simulation Results

From the Start menu, select All Programs > HyperWorks <version> > HyperGraph.
Click Build Plots .
Click the file browser and load the InvertedPendulum_NoCosimulation.mrf file. This was the baseline result created by running MotionSolve by itself.
In the Page Controls toolbar, create two vertical plot windows.

Figure 9. Create Two Plot Windows
Select Marker Displacement for Y-Type, REQ/70000004 Output slider displacement (on Slider cart) for Y Request, and DX for Y Component to plot the cart's translational displacement:

Figure 10. Plot the Cart's Displacement
Select the window on the left and click Apply.
Select Marker Force for Y-Type, REQ/70000002 Output control force- (on Slider cart) for Y Request, and FX for Y Component to plot the X component of the control force:

Figure 11. Plot the Control Force on the Cart
Click the file browser icon and load the InvertedPendulum_Cosimulation.mrf file. This was the co-simulation results run with Simulink.
Select Marker Displacement for Y-Type, REQ/70000004 Output slider displacement (on Slider cart) for Y Request, and DX for Y Component to overlay the plot in the left window.
Select Marker Force for Y-Type, REQ/70000002 Output control force- (on Slider cart) for Y Request, and FX for Y Component to overlay the plot in the right window.
Both the signals match as shown below.

Figure 12. Comparison of the Cart Displacement and Cart Control Force Between the Two Models

The blue curves represent results from the MotionSolve-only model and the red curves represent results from the co-simulation.