Motion: PASSIVE_RIGID_BODY
It is possible to define a rigid body motion in nanoFluidX such that the body is freely interacting with the fluid (exchanging momentum and heat with the fluid).
In order to define such motion as generally as possible, a number of parameters have to be set in Imposed motions.
PASSIVE_RIGID_BODY motion define the standard 6-DOF motion and constrains motion in a number of ways, and also includes linear and torsional spring forces which act on the body. PASSIVE_RIGID_BODY offers parameters that can be set for this type of motion. Some of the commands are simple and can be considered self-explanatory (for example, body_mass, init_CoM, init_vel), but others require clarification.
Depending on the complexity of the case and the data you have available, you may need to specify 0, 1, or 2 additional coordinate systems.
The Cartesian coordinate system, which is commonly referred to as a global coordinate system or global reference frame, is the default coordinate system in which the code is operating and does not need a definition. It is assumed that it coincides with the inertial frame of reference.
- mom_principal_ax_x_i "x y z"
- mom_principal_ax_y_i "x y z"
- mom_principal_ax_z_i "x y z"
where the “x y z” coordinates represent the unit vectors expressed in global coordinates. The suffix “i” at the end of the command stands for “inertial”, to indicate which coordinates to use when defining the unit vector components.
- prbcon_ax_x_i "x y z"
- prbcon_ax_y_i "x y z"
- prbcon_ax_z_i "x y z"
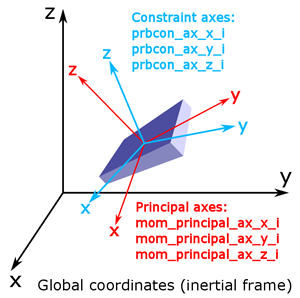
Figure 1. Coordinate Systems used for PASSIVE_RIGID_BODY and the Respective Definition Commands. In general, it is not necessary for the three coordinate systems to align.
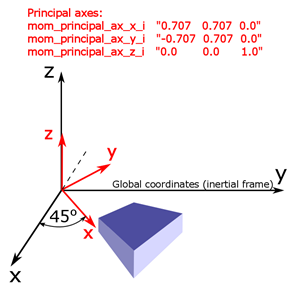
Figure 2. Hexagonal Body Rotated by 45 Degrees around the Z-Axis. Appropriate commands are used to define the principal axes coordinate system.
The exact same principle can be applied to the constraint coordinate system if you, for example, wish to constrain the motion of the body in the direction that is under 45 degrees with respect to the global x or y axes.
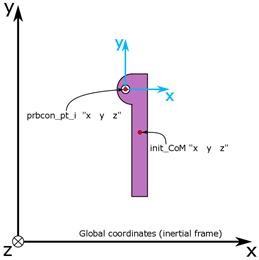
Figure 3. 2D Hinge. This example shows how to define a new coordinate center for the constraint coordinate system using prbcon_pt_i command.
Linear or torsional springs can also be defined. To illustrate the basic concept of such a setup, refer to Figure 4. The example shows the setup of a body which is hanging on a spring. The initial location of the body does not correspond to the equilibrium point of the spring, that is to say that you have a pre-deformation of the spring (prbcon_linspr_p_c) when starting the simulation. Along with this you of need to set the stiffness coefficient of the spring (prbcon_angspr_k_c). Between these two parameters you can define a force that is initially acting on the spring. Same principles apply for torsional springs, except that the deformation is expressed in [rad], and the stiffness of the spring in [Nm/rad].
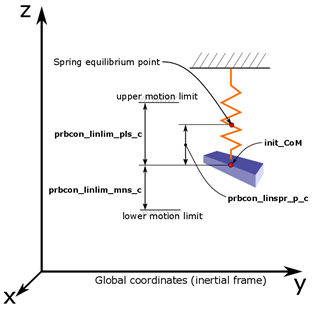
Figure 4. Linear Spring Setup with Annotated Commands
Rigid-rigid body or wall-rigid body interactions are not supported. It is possible to simulate more than one rigid body in the domain, but their interactions are not modeled.
Also, a rigid body cannot cross a PERIODIC boundary.
With passive rigid body motion it is also possible to prescribe constant force or torque acting on a body by using prbcon_cnstfrc_c or prbcon_cnsttrq_c.
Alternatively the user can prescribe either constant or varying linear or angular velocities to each of the bodies by using prbcon_linvel_* and prbcon_angvel_* sets of commands.