logint

Syntax

logint(old_x, old_y, new_x, flag)

Argument

Example

Flag 0 results in both axes ben logarithmically scaled.

Figure 1.

Flag 1 works if only one X axis is logarithmically scale. The Y axis is linearly scale.

Figure 2.

Flag 2 works if only one Y axis is logarithmically scaled. The X axis is linearly scale.

Figure 3.

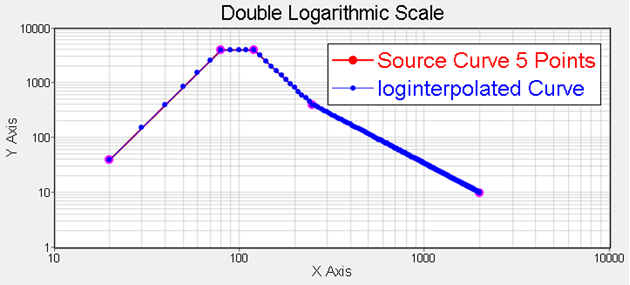
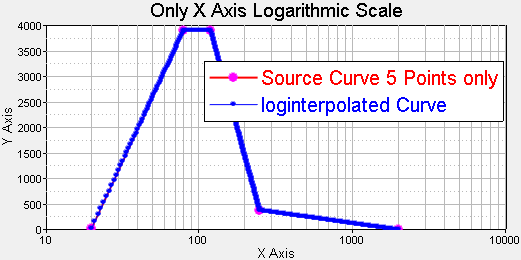
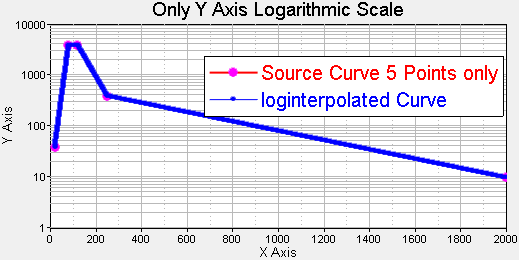
Curve Math Vectors	Results
x = new_x y = logint(c1.x, c1.y, new_x)	Given c1, a curve is created with interpolated y values at each point of new_x.

Comments

The logint function uses linear interpolation to resample data. logint estimates a y-value for each element in new_x such that the new points lie on or near the curve defined by old_x, old_y. old_x, old_y and new_x must have the same number of elements.

If old_x is not entirely increasing and new_x is a scalar, the first value of old_x is used. If new_x is a vector, old_x must be entirely increasing.

If new_x is a scalar, the result is a scalar. If new_x is a vector, the result is a vector with the same number of elements as new_x.

logint performs interpolation only. All values of new_x must lie between the minimum of old_x and the maximum of old_x.