Multi - Objective Genetic Algorithm (MOGA)
An extension of Genetic Algorithm that solves multi-objective optimization (MOO) problems.
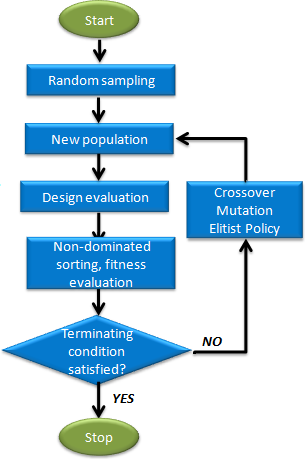
In MOO problems, there is more than one objective function to be minimized or maximized and as such the goal is not to find an optimum but to find the Pareto front instead. Pareto front is a collection of non-dominated designs. Non-dominated designs are better than other designs because at least one of the objective functions are considered.
Usability Characteristics
- Multi - Objective Genetic Algorithm uses a crowding distance metric to create a homogeneous distribution of the non-dominated points on the Pareto front.
- Multi - Objective Genetic Algorithm terminates if one of the conditions below are
met:
- The convergence criteria is satisfied. This occurs when the minimum number of allowable iterations (Minimum Iterations) are run, feasible designs are found (Constraint Violation Tol. (%)), and the non-dominated designs did not change in the last iteration.
- The maximum number of allowable iterations (Maximum Iterations) is reached.
- An analysis fails and the Terminate optimization option is the default (On Failed Evaluation).
- Supports input variable constraints.
- Although the number of evaluations per iteration is a combination of multiple settings, it is primarily affected by the Population Size setting. All evaluations within an iteration may be executed in parallel. If parallel computing is required, it is recommended to use the Meta-Model or No Hybrid method.
Settings
| Parameter | Default | Range | Description |
|---|---|---|---|
| Maximum Iterations | 50 | >0 | Maximum number of iterations allowed. |
| Minimum Iterations | 25 |
|
Processes at least Minimum Iterations iteration steps. Use this setting to prevent pre-mature convergence. By setting Minimum Iterations to be the same as Maximum Iterations, the defined number of iteration steps will be run. Multi - Objective Genetic Algorithm will be terminated if it has iterated the minimum iteration steps and feasible designs are found and the non-dominated designs did not change in the last iteration. |
| Population Size | 0 | Integer > 1 |
If Population Size is 0, then
population size is calculated according to the following equation, where
N is the number of input variables.
Population Size=[3+37e−(N−15.806)0.5]N
If the allowable
computational effort is limited, set your own value.
Tip: In
general, it is better to process at least 25 iteration
steps.
|
| On Failed Evaluation | Ignore failed evaluations |
|
|
| Parameter | Default | Range | Description |
|---|---|---|---|
| Crowding Distance | Design Space |
|
Determines in which space the crowding distance is
evaluated. The crowding distance evaluation strategy
allows users to get solutions more uniformly distributed in
the selected space.
|
| Discrete States | 1024 | Integer > 1 |
Number of discrete values
uniformly covering the range of continuous variables including upper and
lower bound.
Tip: Select as a power of 2, for example 64 =
2^6, 1024 =2^10, and so on.
A larger value allows for higher
solution precision, but more computational effort is needed to find the
optima. |
| Mutation Rate | 0.01 | 0.0 - 1.0 |
Mutation rate (probability).
Larger values introduce a more random effect. As a result, the algorithm
can explore more globally but the convergence could be slower.
Tip: Recommended range: 0.001 – 0.05
|
| Elite Population (%) | 10 | 1.0 - 50.0 |
Percentage of population
that belongs to elite. The one with highest fitness value is directly
passed to the next generation. This is a very important strategy, as it
ensures the quality of solutions be non-decreasing. A larger value means
that more individuals will be directly passed to the next generation,
therefore new gene has less chance to be introduced. The convergence
speed could be increased. The drawback is that too large of values could
cause premature convergence.
Tip: Recommended range: 1.0 –
20.0.
|
| Random Seed | 0 | Integer 0 to 10000 |
Controlling repeatability of
runs depending on the way the sequence of random numbers is
generated.
|
| Number of Contenders | 2 | Integer 2 to 5 |
Number of contenders in a tournament selection. For larger values, individuals with lower fitness value have less chance to be selected. Thus, the good individuals have more chance to produce offspring. The bad effect is that, diversity of the population is reduced. The algorithm could converge prematurely. |
| Penalty Power | 1 |
|
Penalty power in the
formulation of the fitness function as exterior penalty function.
Tip: Recommended range: 1.0 – 2.0.
|
| Penalty Multiplier | 2.0 | > 0.0 |
Initial penalty multiplier
in the formulation of the fitness function as exterior penalty function.
Penalty multiplier will be increased gradually with iterating steps
going on. In general, larger values allow the solution to become
feasible with less iteration steps; but too large of a value could
result in a worse solution.
Tip: Recommended range: 1.0 –
5.0.
|
| Distribution Index | 5 | Integer 1 to 100 |
Distribution index used by real coded Multi - Objective Genetic Algorithm. Controls offspring
individuals to be close to or far away from the parent individuals.
Increasing the value will result in offspring individuals being closer
to the parents.
Tip: Recommended range: 3.0 –
10.0.
|
| Type | Real | Real or Binary |
|
| Max Failed Evaluations | 20,000 | >=0 | When On Failed Evaluations is set to Ignore failed evaluations (1), the optimizer will tolerate failures until this threshold for Max Failed Evaluations. This option is intended to allow the optimizer to stop after an excessive amount of failures. |
| Hybrid Algorithm | No hybrid |
|
|
| Use Inclusion Matrix | No |
|
|