Task Analysis

In MotionView, models are assembled from libraries of pre-defined systems using the Assembly Wizard. The Assembly Wizard dialog guides you through the assembly process, ensuring that your selections are compatible.
  1. Click Analysis → Task Wizard.


    Figure 1.
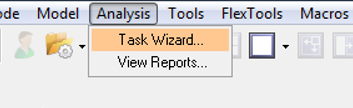    The Task Wizard – Component Analysis window opens.


    Figure 2.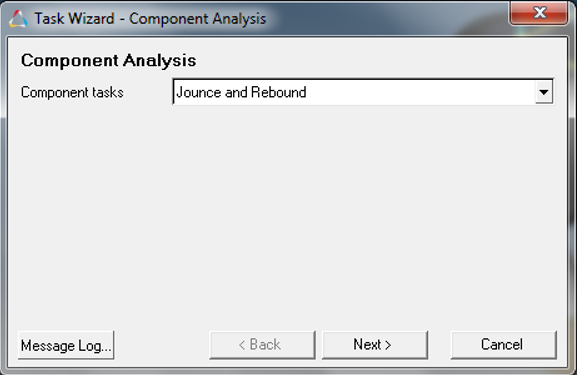
  2. Select the required option in the Component tasks drop-down menu and click Next.
  3. Now you have selected the required analysis data for the model, click Finish button to complete the process and exit Task Wizard.


    Figure 3.
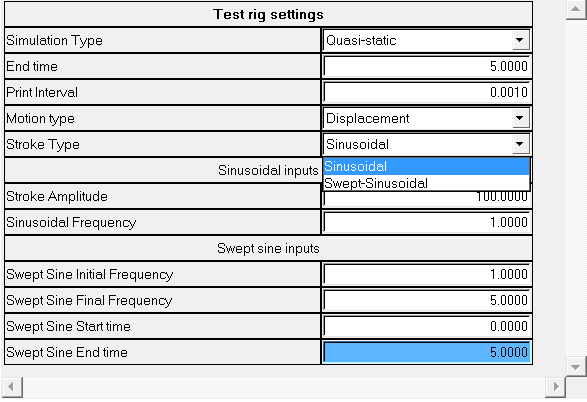
  4. Select the required options in the Test Rig settings section.


    Figure 4.
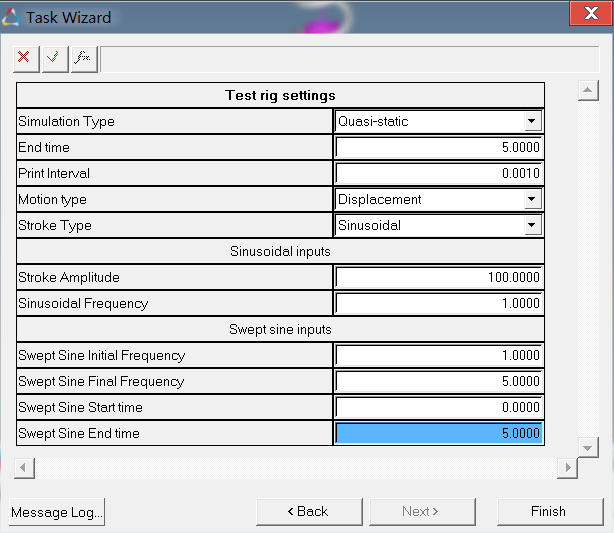
  5. Select Transient or Quasi-Static option from the Simulation Type drop-down menu and select the sinusoidal or swept-sinusoidal option from the Stroke Type drop-down list and enter the required values in the Sinusoidal inputs and Swept sine inputs sections, then click Finish.


    Figure 5.
    It is important to note here that a Transient analysis is needed if you wish to plot damper velocity characteristics.
    Note: In the component test rig, you can simulate the impact of road excitations on the suspension by selecting one of the options in the Motion type drop-down in the Analysis Wizard. The motion is applied to the axle in the test rig. Currently, the following two options are supported:
    Sinusoidal Input
    Sinusoidal input allows the user to apply a time-invariant frequency based displacement/velocity to understand the response of the suspension. The response is governed by the following equation,

    Y=A sin(ωt)

    Where, A is the amplitude of the stroke, ω is the constant angular frequency and t is the current time.

    Swept-Sinusoidal Input
    Swept sinusoidal input allows the user to apply a time-variant frequency to the axle. The swept sinusoidal response is governed by the following equation,

    Y=A sin(thetha(t))

    where A is the amplitude, and thetha(t) =

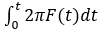
    Based on the values, input for the start and end time for swept sine analysis by the user, F(t) is considered to vary according to the following equations.

    F(t)=0 0<t< tstart

    F(t)=ωinit + (ωfinal - ωinit)(t-tstart) tstart < t < tend

    F(t) = ωfinal t > tend

    For the time starting from tstart to tend, the frequency is assumed to vary linearly from ωinit to ωfinal.



    Figure 6.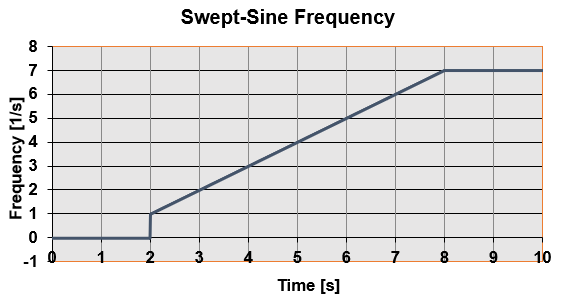

    The above graph shows an example of a frequency input where the frequency varies linearly from 1Hz at t=2sec to 7Hz at t=8sec.