Tire Contact Methods

Tire contact methods calculate the tire penetration, contact patch location, etc. which are used by tire models to calculate forces and moments. There are two contact methods available with MotionSolve:
  • Single Point Contact
  • Elliptical Cam Contact Model
Note: Additional information about the tire carcass shape can be provided in the tire property file which can be used by any of the contact methods for the contact patch location calculation.

Single Point Contact

This is the default contact method that is used with the Fiala model. This model assumes the "disc" shape for the tire and rim and calculates the contact point at the intersection of the wheel plane with the road tangent.

Motorbike tires have more curvature when compared with a car tire. At an inclination angle, the theoretical contact point shifts in the lateral direction. The geometry of the tire carcass is used to model this behavior.



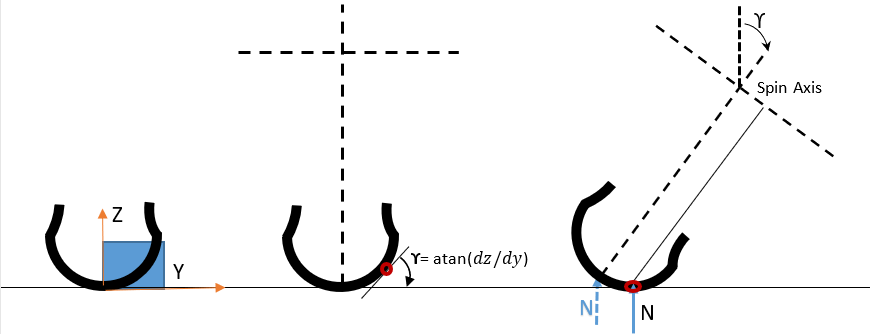
Figure 1. From left: Tire cross section data needed for contact point evaluation | Tire at 0 camber angle | Tire at ϒ camber angle
The parameters required for the contact point evaluation are shown in the table below:
Parameters Details Unit
PA1 Coefficient of the square root term in the contact length equation. -
PA2 Coefficient of the linear term in the contact length equation. -
SECTION_PROFILE_TABLE Table containing Z vs Y data of the tire cross section. Length - Length

PA1 and PA2 shows the variation of contact patch length and width respectively. The size of the contact patch increases with increasing vertical load. The dimensions of the contact patch can be obtained by pressing the tire on carbon paper or by using ink.

Contact Length Equation:

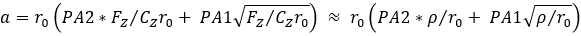
Contact Width Equation:

Where a, b are effective half-length and half-width of the contact patch.

is the width of the tire.

The SECTION_PROFILE_TABLE contains the data of the tire carcass. The table should contain two columns as shown below:



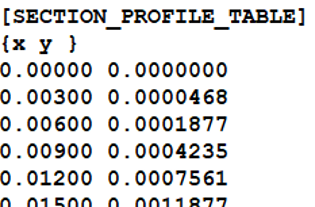
The {x y} in the above table serves as the label. The table is read as per the TYDEX-W coordinate system and it represents the height variation of carcass with respect to points along the carcass width. Data for only a quarter of tire carcass is needed as the tire is assumed symmetric about XY plane in ISO system. The data points should be monotonically increasing otherwise data points will be ignored and the tire contact with will be calculated assuming a rectangular tire carcass.

Elliptical Cam Contact Model

To predict the nonlinear rolling behavior of a tire over an obstacle shorter than the contact patch, a geometric filter is created using a series of parallel cams distributed over the contact patch. These cams displace vertically according to the road height variation. The center of the cams is used to create a virtual plane which is called effective road surface plane. The orientation of this effective road surface plane is defined such that the resulting force that would act on tire is directed normal to the effective road plane. The following characteristics of road surface are captured:
  • Effective road height variation
  • Effective slope variation
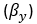
  • Effective curvature
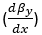
  • Camber change
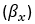
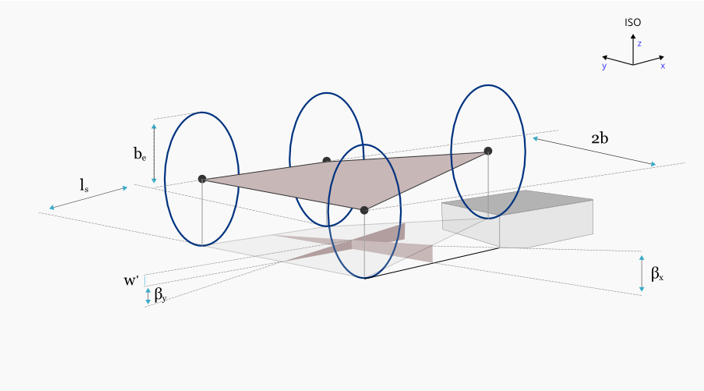
The 3D arrangement looks like the one shown in the image below:


Figure 2. 3D Elliptical Cam Contact Arrangement
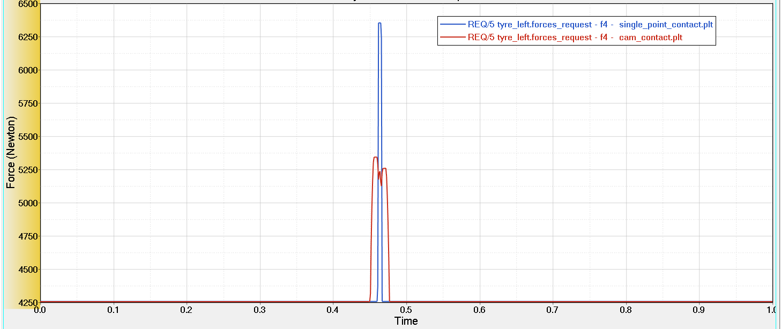
Based on the above variations the forces are calculated using FIALA algorithm. The images below show the difference in calculated force when using a single point contact versus cam contact model.


Figure 3. Vertical force at constant axle height when tire is rolled over a cleat (10 mm height, 50 mm length) at constant velocity of 10.833 m/sec (39km/h)


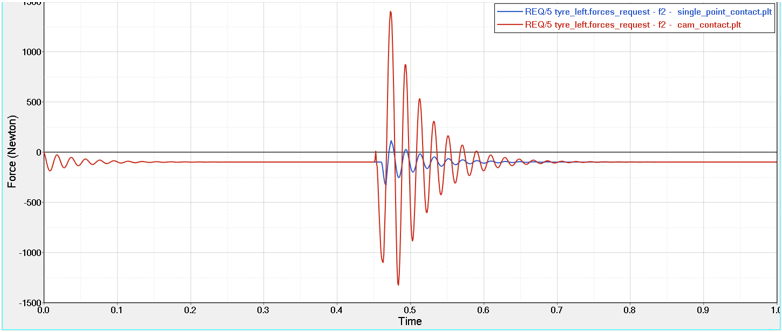
Figure 4. Longitudinal force at constant axle height when tire is rolled over a cleat (10 mm height, 50 mm length) at constant velocity of 10.833 m/sec (39km/h)

The results show that single point contact model predicts higher values of vertical force because it traces the obstacle, however the actual force experienced by the tire is less which is closely predicated using cam contact method.

The tire’s outside contour when rolling over an obstacle matches closely to the ellipse shape. In fact, by measuring the contour one can decide on the ellipse dimension that is needed for the cam contact model.


Figure 5. Filtered Road Profile Using a Series of Cams

How to Use a Cam Contact Model

To use a cam contact method with Fiala Tire, the following attribute should exist in the [MODEL] block:

CONTACT_MODEL = '3D_ENVELOPING'

If ‘CONTACT_MODEL’ attribute is not found in [MODEL] block than a single point contact method will be used with FIALA tire. In case the attribute is set to ‘3D_ENVELOPING’ than tire interface will look for a [CONTACT_COEFFICIENTS] block, this block should contain the parameters listed in the table below.
Parameters Details Unit
PA1 Coefficient of the square root term in the contact length equation. -
PA2 Coefficient of the linear term in the contact length equation. -
PB1 Coefficient of the cube root term in the contact width equation. (reserved) -
PB2 Coefficient of the linear term in the contact width equation. (reserved) -
PAE Half of the ellipsoid length. Length
PBE Half of the ellipsoid height. Length
PCE Order of the ellipsoid. -
PLS Scaling of the distance between the front and rear ellipsoid. -
ROAD_INCREMENT Mesh size for the ellipsoid. Length
N_WIDTH Number of cams along the contact width. -
N_LENGTH Number of cams along the contact length. -

PA1 and PA2 show the variation of the contact patch length. The size of the contact patch increases with increasing vertical load. The dimension of the contact patch can be obtained by pressing tire on carbon paper or by using ink.

Contact Length Equation:

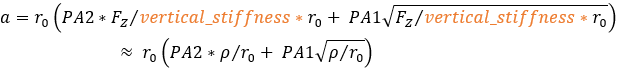
Where 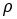is the tire penetration and 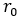is the unloaded radius of the tire.

PB1 and PB2 are not used to calculate the contact patch width.

Contact Width Equation:

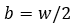
Where a, b are effective half-length and half-width of the contact patch.

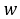is the width of the tire.

The equation for the shape of cam can be written as:



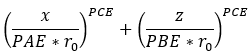
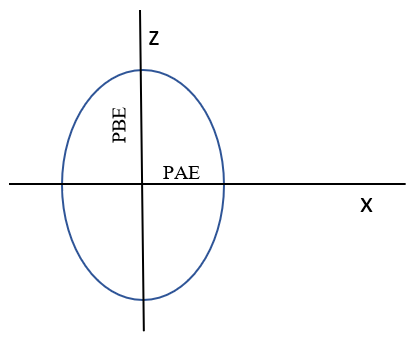
Figure 6. Cam Dimension


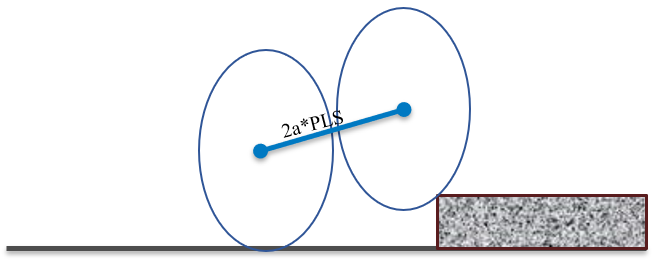
Figure 7. Cam with Two Point Follower

In case no data is available, a good estimate of PAE and PBE is equal to tire radius. The ellipse dimension can be calculated by measuring the outside contour of tire when it touches the obstacle. For PLS a 0.8 is a good value to use. ROAD_INCREMENT decides the meshing size of road it directly affects the computation time of model.