Application Area 5: Multi-objective Optimization
Systems are required to satisfy multiple objectives. These problems require a slightly different approach.
| Minimize | f= [ψ01(x,b),ψ02(x,b),…,ψ0n(x,b)]T | (objective function) |
| Subject to | ψi(x,b) ≥0, i=1, …, p | (inequality constraints) |
|
ψi(x,b)=0, i=p+1, …, m
bL ≤b ≤ bU |
(equality constraints) (design limits) |
The functions ψ(x,b) in the cost and constraint functions are assumed to have the form:
ψ(x,b)= ψ0(x,b)+Tf∫T0L (x,b) dt
| Minimize: | f= ∑nj=0wjψ0j(x,b) | (objective function) |
| Subject to: |
ψi(x,b)≥0,i=1,…,p
ψi(x,b)=0,i=p+1,…,m bL ≤b ≤ bU |
(inequality constraints) (equality constraints) (design limits) |
wj>0 are a set f weights that reflect the relative importance of the various objectives.
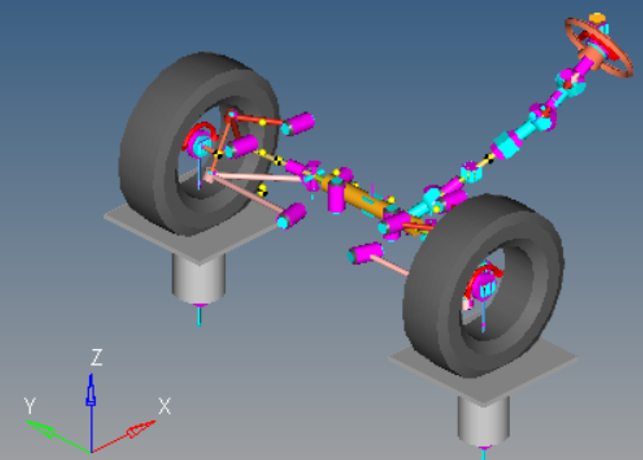
Example 1
- Design Goal
- Considering a kinematic SLA suspension, the design goal is to modify hard points in a suspension to obtain desired ride behavior.
- Ride Steer @ Design = -4°/m
- Ride Steer @ Full Jounce = -4°/m
- Ride Camber @ Design = +5°/m
- Ride Camber @ Full Jounce = +5°/m
- Ride Caster @ Design = -8°/m
- Ride Caster @ Full Jounce = -8°/m
Ride Steer = ∂ steerAngle ∂ rideHeight
Ride Camber = ∂ steerAngle ∂ rideHeight
Ride Caster = ∂ casterAngle∂ rideHeight
- Design Variables
- Various hard point locations in the suspension are available as design
variables. For this problem, there are 26 design variables.
Upper Control Arm Inboard hard-points (Fore/Aft) XYZ (6 DV) Lower Control Arm Inboard hard-points (Fore/Aft) XYZ (6 DV) Upper Ball Joint hard-point XYZ (3 DV) Lower Ball Joint hard-point XYZ (3 DV) Tie rod Inner & Outer XYZ (6 DV) Spindle Alignment Point Location XZ (3 DV) - Results
- For this example, the optimization method worked quite well.
Response Target Actual Ride Steer @ Design -4 °/m -4.107 °/m Ride Steer @ Full Jounce -4 °/m -3.898 °/m Ride Camber @ Design +5 °/m +4.937 °/m Ride Camber @ Full Jounce +5 °/m +5.024 °/m Ride Caster @ Design -8 °/m -8.402 °/m Ride Caster @ Full Jounce -8 °/m -7.594 °/m
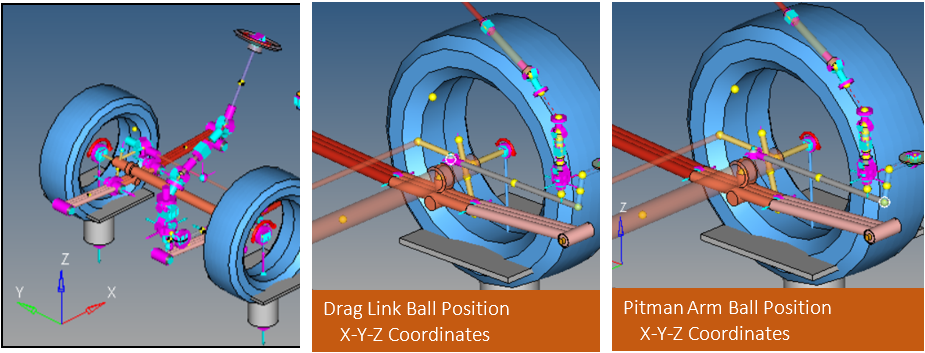
Example 2
- The left and right wheels have zero steer when the steering wheel angle is zero.
- The steering angle difference between the left and right wheels should be zero at maximum steer and minimum steer.
- Steering ratio refers to the ratio between the turn of the steering wheel and the turn of the wheels. The steering ratio at zero steering wheel angle is required to be 9.27.
- Left Wheel Steer Angle @ zero Steering Wheel Angle =0
- Right Steer Angle @ zero Steering Wheel Angle =0
- Steer Angle Difference between left and right wheels = 0
- Steering Ratio @ Zero Steering Wheel Angle = 9.27
- Design Variables
-
- Drag Link Ball Position X-Y-Z Coordinates
- Pitman Arm Ball Position X-Y-Z Coordinates
- Results
- For this example, the optimization method worked quite well. The results
obtained are shown below:
Response Target Actual Left Steer @ Zero SWA 0° +0.001° Right Steer @ Zero SWA 0° +0.000° Steering difference (L vs. R) 0° -0.003° Steering ratio @ Zero SWA 9.27 9.271