HTire Modeling Approach
Rolling Kinematics
- tire deflection and tire deflection velocity
- longitudinal slip
- side-slip angle
- turn slip
- camber angle
Contact Computation and Coupling to COSIN/Road
Tire deflection and tire deflection velocity are determined using the point contact approach with a certain built-in low-pass filter effect. This effect is achieved by choosing a large step-size in applying numerical differentiation for the road tangent plane computation. The large step-size smooths sharp changes in road inclination.
Alternative Non-Linear Radial Stiffness Model and Bottoming
As an alternative to the standard constant radial stiffness approach, HTire has the ability to specify arbitrary data pairs for the deflection-load characteristic, which are interpolated by a smooth spline.
By extending these data into the region of extreme deflection, also bottoming effects in misuse situations can easily be taken into account.
Zero Velocity Capability
Moreover, HTire uses a certain numerical modification of the slip quantities at very small forward speed, to deal with the well-known slip singularities in such operating points. At even smaller speed, HTire switches smoothly to a model variant for standing condition, being able to keep the vehicle completely standing even on inclined roads, if the park brake is engaged.
Thanks to these modifications, HTire does not show any numerical instability during stand-still. However, the modification might result in a certain small but non-zero sliding velocity when the vehicle is parking on an inclined road, even if the wheels are blocked.
Combined Slip Modifications
The 1989 version of Magic Formula initially did not comprise a combined slip approach. However, a respective modification had been added to the equations in HTire, making use of a simple friction ellipse approach.
The same approach can, as an option, also be used in the 2002 variant, eventually replacing the detailed combined-slip model suggested by Pacejka. This replacement might be helpful if only limited measurement data are available, which might be insufficient for a respective data fit.
Tire Lag and Relaxation Length
Both MF variants are completed with a non-linear first order transient force lagging approach. With the kind of non-linearity used, it is taken into account that the decrease in contact forces might take place faster than a respective increase. This effect introduces a certain frequency-dependency of the mean tire force decrease, if wheel load variations apply.
Mathematically, the non-linear tire lag is described by the following non-linear first order differential equation, used for side force, longitudinal force, and aligning torque:
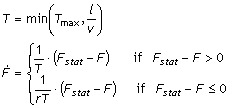
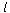 is the constant relaxation length
is the constant relaxation length is the time dependent rolling speed
is the time dependent rolling speed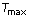 is the constant upper bound for the resulting time
constant
is the constant upper bound for the resulting time
constant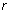 is a reduction factor, describing the relation between time
constant for force increase and time constant for force decrease
is a reduction factor, describing the relation between time
constant for force increase and time constant for force decrease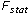 is the stationary value of the respective force or torque
(longitudinal force, side force, or aligning torque, respectively)
is the stationary value of the respective force or torque
(longitudinal force, side force, or aligning torque, respectively) 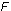 is the resulting transient value of this force or torque
is the resulting transient value of this force or torque