I-deas

These checks apply to both types of elements, but when applied to 3D elements they are generally applied to each face of the element. The value of the worst face is reported as the 3D element’s overall quality value.

Stretch (Aspect Ratio)

Stretch is evaluated differently depending on whether the element is triangular or quadrilateral:

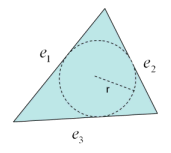
• For trias, the radius of the largest circle that fits within the element is divided by the longest edge, then multiplied by the square root of 12.

  
  
  

  $stretch=\sqrt{12}\times \frac{r}{e_{\max }}$

  Figure 1. Stretch for Trias

• For quads, the minimum edge length is divided by the maximum diagonal length. The result is multiplied by the square root of 2.

Note: The inverse of stretch displays on-screen in HyperWorks as the aspect.

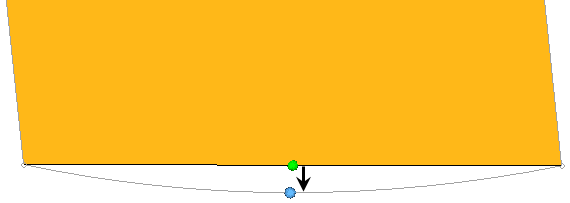
Chordal Deviation

Largest distance between the centers of element edges and the associated surface. Second order elements return the same chordal deviation as first order, when the corner nodes are used due to the expensive nature of the calculations.

Figure 2. Chordal Deviation

Jacobian

Deviation of an element from its ideal or "perfect" shape, such as a triangle’s deviation from equilateral. The Jacobian value ranges from 0.0 to 1.0, where 1.0 represents a perfectly shaped element. The determinant of the Jacobian relates the local stretching of the parametric space which is required to fit it onto the global coordinate space.

HyperWorks evaluates the determinant of the Jacobian matrix at each of the element’s integration points, also called Gauss points, or at the element’s corner nodes, and reports the ratio between the smallest and the largest. In the case of Jacobian evaluation at the Gauss points, values of 0.7 and above are generally acceptable. You can select which method of evaluation to use (Gauss point or corner node) from the Check Element settings.

Length (min)

Minimum element lengths are calculated using one of two methods:

• The shortest edge of the element. This method is used for non-tetrahedral 3D elements.
• The shortest distance from a corner node to its opposing edge (or face, in the case of tetra elements); referred to as "minimal normalized height".

Figure 3. Length (min)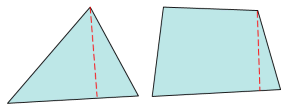

Skew

Deviation of an element’s corners from 90 degrees (for quads) or 60 degrees (for trias).

The check calculates skew by finding:

• $={\displaystyle \sum _{i=1}^4\left|90-{\alpha }_i\right|}$ for quadrilaterals
• $={\displaystyle \sum _{i=1}^3\left|90-{\alpha }_i\right|}$ for triangular elements

Where alpha is the angle of each corner. An ideal/equilateral element has a skew of zero, as none of its corners deviate from the target (90 or 60 degrees).

Taper

Taper ratio for the quadrilateral element is defined by first finding the area of the triangle formed at each corner grid point.

Figure 4. Taper

These areas are then compared to one half of the area of the quadrilateral.

HyperWorks then finds the smallest ratio of each of these triangular areas to ½ the quad element’s total area. In the diagram above, "a" is smallest. The resulting value is subtracted from 1, and the result reported as the element taper. This means that as the taper approaches 0, the shape approaches a rectangle.

$taper=1-{{\displaystyle \left(\frac{A_{tri}}{0.5\times A_{quad}}\right)}}_{\min }$

Triangles are assigned a value of 0, in order to prevent HyperWorks from mistaking them for highly-tapered quadrilaterals and reporting them as "failed".

Warpage

The amount by which an element, or in the case of solid elements, an element face, deviates from being planar. Since three points define a plane, this check only applies to quads. The quad is divided into two trias along its diagonal, and the angle between the trias’ normals is measured.

Stretch (volume aspect ratio)

Stretch is evaluated differently depending on whether the element is a tetrahedron, Wedge, Brick, or Pyramid.

Tetras

The radius of the largest sphere that fits within the element is divided by the longest edge. This value is then multiplied by the square root of 24.

Wedges

Each face is evaluated for its 2D stretch, and the worst value is reported. This means that the value reported for vol AR should always be the same as that reported for aspect.

Bricks

The minimum edge length is divided by the maximum diagonal length. The result is multiplied by the square root of 3.

Pyramids

No check is defined, so HyperWorks performs its standard check in which each face is evaluated as a 2D object and the worst result reported.