/MAT/LAW78

During the plastic deformation, a yield surface will move within the bounding surface and will never change its size, and the bounding surface can change both in size and location. The plastic-strain dependency of the Young's modulus and the work-hardening stagnation effect are also taken into account. Concerning SPH, it is compatible with solid only, this can be verified with the /SPH/WavesCompression test. The solid version is only isotropic. The shell version is anisotropic based on Hill criterion.

Format

Definitions

Example

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                 Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW78/1/1
DP600-HDG
#              RHO_I
              7.8E-9
#                  E                  NU
              206000                  .3
#                  Y                   B                   C                   H                  B0
                 420                 112                 200                   0                 555
#                  m                RSAT      OPTR                  C1                  C2
                  12                 190         0                   1                   1
#                 R0                 R45                 R90
                   1                   1                   1
#  fct_IDE                          EINF                  CE
         0                             1              163000
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

1. For solid elements, von Mises yield criterion is used, so the yield function is expressed as:(1)
   $$f=\frac{3}{2}\left(\mathbf{s}-\mathbf{\alpha }\right):\left(\mathbf{s}-\mathbf{\alpha }\right)-Y^2$$
   Whereas for shell elements, Hill's (48) yield criterion is used, which allows modeling anisotropic materials and it is expressed as:(2)

   $$f=\phi (\mathbf{\sigma }-\mathbf{\alpha })-Y^2$$
   Where, ( $\phi$ ) is expressed as:(3)

   $$\phi (A)=A_{xx}^2-\frac{2r_0}{1+r_0}{A}_{xx}{A}_{yy}+\frac{r_0\left(1+r_{90}\right)}{r_{90}\left(1+r_0\right)}{A}_{yy}^2+\frac{r_0+r_{90}}{r_{90}\left(1+r_0\right)}\left(2r_{45}+1\right)A_{xy}^2$$
2. Yield stress, Poisson ratio and Young's modulus should be strictly positive. The other parameters should be non-negative value.
3. The schematic illustration of the two-surface model is shown in Figure 1.
   Where, 0 is the original center of the yield surface, the yield surface with its center $\alpha$ and its radii Y, is moving kinematically, within a bounding surface that has a size indicated by B+R and tensor $\mathbf{\beta }$ indicating its center position.

   
   
   Figure 1. Schematic Drawing of the Two-surface Model

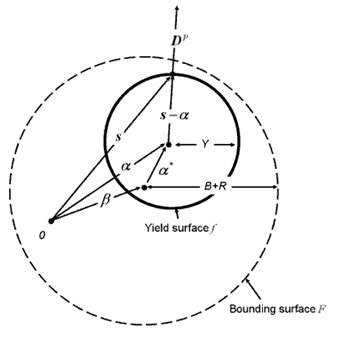
4. The yield surface is subjected to a kinematic hardening. The kinematic motion is described by ${\mathbf{\alpha }}^{*}$ that has the following evolution:

   ${\dot{\alpha }}^{*}=C\left[\left(\frac{a}{Y}\right)\left(\mathbf{\sigma }-\mathbf{\alpha }\right)-\sqrt{\frac{a}{\Vert {\mathbf{\alpha }}^{\text{*}}\Vert }}{\mathbf{\alpha }}^{*}\right]{\dot{\overline{\epsilon }}}_p$

   for shell elements

   ${\dot{\alpha }}^{*}=C\left[\left(\frac{2}{3}\right)a{\dot{\epsilon }}_{{}^{\mathbf{p}}}-\sqrt{\frac{a}{\Vert {\mathbf{\alpha }}^{*}\Vert }}{\mathbf{\alpha }}^{*}{\dot{\overline{\epsilon }}}_{{}^P}\right]$

   for solid elements

   Where,

   • ${\dot{\overline{\epsilon }}}_p$ is the equivalent plastic strain rate
   • C and a are material parameters. And $a=B+R-Y$
   • $\mathbf{\alpha }={\mathbf{\alpha }}^{*}+\mathbf{\beta }$ is the total back stress
5. The bounding surface is subjected to an isotropic-kinematic hardening. The evolution equation for isotropic hardening is:

   $\dot{R}=m\left(R_{\mathit{sat}}-R\right){\dot{\overline{\epsilon }}}_{{}^p}$

   Default (if OptR = 0) Yoshida expression

   $R=R_{\mathit{sat}}\left[{\left(C_1+{\overline{\epsilon }}_{{}^p}\right)}^{C_2}-C_1^{C_2}\right]$

   Available for shell elements, if OptR = 1

   The evolution equation for kinematic hardening of bounding surface is:(4)

   $$\dot{\mathit{\beta }}=m\left(\frac{2}{3}b{\dot{\epsilon }}_{\mathbf{p}}-\mathit{\beta }{\dot{\overline{\epsilon }}}_{{}^p}\right)$$
6. The work-hardening stagnation during unloading is described using a J₂-type surface $g_{\sigma }$ with a radius r and a center q:(5)
   $$\begin{array}{l}{g}_{\sigma }(\mathbf{\beta },{\mathbf{q}}^{\prime },r)=\frac{3}{2}(\mathbf{\beta }-{\mathbf{q}}^{\prime }):(\mathbf{\beta }-{\mathbf{q}}^{\prime })-r^2\\ {\dot{\mathbf{q}}}^{\prime }=\text{μ}\left(\mathbf{\beta }-{\mathbf{q}}^{\prime }\right)\\ r=h\dot{\Gamma }\hspace{0.17em},\dot{\Gamma }\frac{3\left(\mathbf{\beta }-{\mathbf{q}}^{\prime }\right):\dot{\beta }}{2r}\end{array}$$

   Where, $\mathbf{\beta }$ should be either inside or on the surface $g_{\sigma }$ .

7. The evolution of Young's modulus:
   • If fct_ID_E > 0, the curve defines a scale factor for Young's modulus evolution with equivalent plastic strain, which means the Young's modulus is scaled by the function $\mathrm{f}\left({\overline{\epsilon }}_p\right)$ :
     • $E\left(t\right)=E\cdot \mathrm{f}\left({\overline{\epsilon }}_p\right)$

     The initial value of the scale factor should be equal to 1 and it decreases.

   • If fct_ID_E = 0, the Young's modulus is calculated as:(6)

     $$E\left(t\right)=E-\left(E-E_{\mathit{inf}}\right)\left[1-\exp \left(-C_E{\overline{\epsilon }}_p\right)\right]$$

     Where,

     E and E_inf are respectively the initial and asymptotic value of Young's modulus, ${\overline{\epsilon }}_p$ is the accumulated equivalent plastic strain.

     Note: If fct_ID_E = 0 and C_E = 0, Young's modulus E is kept constant.
8. This material law is not available for implicit analysis.